- When I use the term ninedigital in these articles I always refer to a strictly zeroless pandigital (digits from 1 to 9 each appearing just once).
Fifth Page
Topic 5.13 [ July 15, 2015 ]
Finding a ninedigital as a substring in the decimal expansion
of that same ninedigital raised to a power p
Here I am looking for
ninedigitals raised to a power
p so that the same
ninedigital pops up as a substring in the decimal expansion of that number.
For that purpose I use UBASIC. One limitation here is that for the largest
ninedigital an overflow occurs when p is greater than 119. Someone who
is equipped with better tools can raise that exponent to higher values and,
no doubt, will certainly find much more solutions. Good hunting!
P@rick.
See WONplate 195 for the pandigital version of this topic.
125387649 116 =
24977680256511635554308807465784640450873233766747803697457826665337615090115
65231746558064246784915939331799792083405477295137019822599431230243339336256
71036099290638462808759659688825404030171009447306472501571623792897838640534
77085356208869947832016110312264802555478542369431139240340476254337276270686
34662823179078224977906450230607287868664539203911690841768842604378676955543
90100851394887980264901371704943840980429647269197342633254961700394120603361
43842807514599611962386883891826228850335619243196918128762543471635650559682
38318742855037099538294619343456338486825737070338628267534489179698733254887
09140884645181171985004192856213046111681831479406534681094572418253243315232
83754693737121802777642827488524555131566356534189708692077962292682715962963
10951543077827723454799874681321232284394839374645645842281885435452335843550
95833227039437289409212070147169984083138099798709210400021021253876491425914
0643857408857601
|
|
217653498 73 =
45382931250436248017939755904905375074156752993340811447973427529953789857607
32955682451554486827163229743678033027505512286752585680945126547840935996116
54815664694471438604641495185180470978832928274085612674105757197078023302686
63726802021863993886105320204264424109074548867821601860831321946603899915989
29493904262834904701039108240350414664604821797810564424853529625576570072775
66618409001769861258075239997032601466426217653498522505043608739599041141286
06969595596576995845246008728621299765577774490078132467180959116981633437817
8405015126965623686132913457323839428590795742775207720401436156100608
|
|
365127984 56 =
31399785292188574093400788496274173401686979859312394666521792490946925319997
76524136398355426736199589711873651279841242087305377690869763740464625716529
59057594291916954556200100043602722007077744099905403348921821982324181941209
69999260251709925043458412798095491979509046250663030898453529337668960610349
03081409266580407331283046683054359019742088912241401726530525075638795375443
40762300436359126476728589070428637730840695632269631597955668180598026800883
697316427481481216
|
|
365781249 51 =
53002135104434083974295107729733667717040654846476097425485261220328866855852
71504803441128772764357739017148646788411029412276275042922694892434396254143
48793515708522071862882724102364998434235736846330684845034104402120935766976
01022971282572645737276412472217099390944995575161648761003059841167281107930
16137006513587023917737671292908464672118160331833046277362244795625534877968
6368907675806217728711828836944399284008197365781249
|
365781249 101 =
76800719919590078432925071974148597876877854062105916684763833185937781705753
83281476183683178644147316682717375665654255225060926550994397177085801874805
26553609913039442760221214744703267598894728210679926761402337567959581385266
21082622518065798159170419928139324519300943918848638348519415234032122155244
05988689600296989099668088818911186434860869532144452751639276824763624763754
04920817120720345528595874747470398626320900446802670284758650353286638757355
75582076312539413336473920504799681382640754693048217806233753987807634460979
23191578353228051041430597711168265165107287178147986560086750154917731725313
59086749279932313619464359933606406209548895901679912639907567337083903120432
99869965011658567583696528762695114783608021250377198923581674468638379220281
62192471621988626202321698325792844640652321364291819301555023466728895229239
568016394365781249
In both cases the expansion ends with our ninedigital !!
In fact I detected a pattern here as for all exponents +50 (starting with 1) it occurs.
1, 51, 101, 151, 201, ...
Can this phenomenon be explained mathematically ?
Yes, as Alexandru Petrescu does with an elegant proof hereunder.
|
|
Proof
By Alexandru Petrescu (PhD in applied mathematics) [ April 17, 2022 ]
Let a = 365781249. Condition is: 109 | (a51–a) or 109 | a(a50–1). But gcd(a,109) = 1 so 109 | (a50–1).
Factorization: a50–1 = (a–1)(a+1)(a4–a3+a2–a+1)(a4+a3+a2+a+1)(a20–a15+a10–a5+1)(a20+a15+a10+a5+1)
a–1 = 365781248 = 28 x 7 x 17 x 12007 (1)
a+1 = 365781250 = 2 x 57 x 2341 (2)
For any number b having the units digit equal to 9 we have:
b2k = 1 (mod 10) and b2k+1 = 9 (mod 10)
So: a4–a3+a2–a+1 = 1–9+1–9+1 = 5 (mod 10) (3)
a20–a15+a10–a5+1 = 1–9+1–9+1 = 5 (mod 10) (4)
From (1)-(4) we have 29 x 59 = 109 | (a50–1).
Generally 109 | (a50p+1–a) because a50p–1 = (a50)p–1 = (a50–1)(....)
The vertical bar "|" stands for 'divides'
Pari/gp has a simple command for producing the 6 terms of the factorization of our polynomial
(14:00) gp > factor(a^50-1)
%1 =
[ a - 1 1]
[ a + 1 1]
[ a^4 - a^3 + a^2 - a + 1 1]
[ a^4 + a^3 + a^2 + a + 1 1]
[a^20 - a^15 + a^10 - a^5 + 1 1]
[a^20 + a^15 + a^10 + a^5 + 1 1]
|
495126738 61 =
23861578656021269346703174520372315791816251470087567211478523202968124667924
93848688084609784146764549823116272246105113757348275839028643583491902670379
64611114317468350096247548658050991212656177878337691054141810387339185188226
37443389139903195571962109654889436933754829870083357415260689569881177088929
20725614584762139979825699821114369929192812850477252290195382123150020328432
81324949512673878966294790960293349542846852039693433215569689109114314341111
102344236031307150080447721778461888506037971062682424038575401074688
|
|
623479581 83 =
93378199229292611484783069958832018204031360211962347958195478201099393097916
34096128381183555954877721494796498660605839598106441880144452469796271440667
05689066988711351184847509304365224018029344080389906241440975034338043383492
65523244487441047103333380133096323111353945707309764846648779004687899784490
95209825853284627548178988792267472945800848267750379848985027317431251568478
10303914183404736553013121265261006876701288947711222743493437503622840039296
31760526249913511031756985513898026705212045956997380233251890795219842954963
98174803095091720475573906927745701371461428793178627967034408092869119201862
69304525412368590073394987109053612598099858622032202094910455231063705993302
5724027684578757254054582767435966341
|
|
634812579 98 =
45631141858726733466372929460343476150274704363477974505922266227178826889112
03296142625749780118820787364378776141951859373704464157741137151720607037161
59124655023048774995732874441504376314578129603660792575268298258639078264194
85376075066280259241460659377367254814707313855803853251377152515963933782042
82013024297285193725035357126051237614145162756780783309796660052474365080592
57486561925965907731081653418482644904546883539412866892308710063071186726094
04162947833101908631744436257625261404831947239275944162745006380618099565297
96459806577080966775040859019302889640794901252275276440231781404017352377903
60488874615440260964529302179978922299373037300601770829712001588815559136063
48125792841936687381899103964185439346538524710921313754184454000657029185913
07178775895169595052782549109915160489328969529916734441976537436220053655780
8083316053484361
|
|
635781249 101 =
13616930906420442043259405929999866138890181953431470395921699407085117760783
79536986744241462996090516980892457600810938519412701377694639547895160589971
79940437644604969159226080307904671668397831678693666758678744510837077805030
78206504513344786576043188805369174334775868464100758383598453386529564392290
31367832734849277419826252716936311745138781812648300098007290980852223803079
72137771591659178231093099603625082034017722405516753317039980819246827005117
36976451379012331388480253663967821868072501222801850425960780267385323754435
07539416471208237069631672456024450838621340577834346701338003303401309670932
01973176630643853667096489340849126751031165929265273487122455492177758908045
89274046128442756534554210620839547826578936054888844310552044248918565678393
81374739820431481832250271626095365734918171778895773396091917556338935202137
3049410410107226308656963293016421635781249
|
635781249 201 =
29164245973260567384593998725899801391036529801483811790123121455125852321698
22356483494243511951735290740862875830839305968363755966766223109083382183664
88576657374238845416864831751683511906055638926371154956341508787131097544659
79522044789543649215998567411972121286520461446088073616511904873309159121071
74684934306957468357280843825646472100322416427703819568376723780664487397781
36609640440854544270101742492038697981640355680661735059638023384998850172032
66356797551332806280817340906746100461811475325319411146411680855221735010791
53992862953768970337009000514903631071241106546078919582643227455640762805923
03709660963193290082477816666688811748112154031780276816328007053689328670077
19486369454747397333719686514715621111571267203548578415858045081152038488373
19738994264925412594037600610232404954957253834070105970798906085984928801129
90069112802435045442019014381173623658922975667291863467667559295986468544645
95871328306360393761967216238027050306942300675363534043656652175578719662302
89488669296643593144384841208946918403617436312679072638091933929765488568810
57706701231797058492686450589593235151332428321380402982579558838646689565348
91937561213424352699023041796996956645347622484730341432324511585887735175214
61796191282018130190838622236792597334721732103343855693075534342114447377455
01930307417746262714112216038771957185176456937958730457766096901663183790850
21632420423456465784563445754553686156000076963413532065706676351187746174688
24823883482637094613008485441319259453071734490504331011445956738207887289935
52707227273816058424570137298617616776868455983820558158072745229332917127873
20544768174850588910654282156308815210119182479471883285722869803551761642790
5893653672809004042634257177233841040848855367748426195935586032842635781249
In both cases the expansion ends with our ninedigital !!
Here again I detected a pattern as for all exponents +100 (starting with 1) it occurs.
1, 101, 201, 301, ...
Can this phenomenon be explained mathematically ?
Yes, as Alexandru Petrescu does with an elegant proof hereunder.
|
|
Proof
By Alexandru Petrescu (PhD in applied mathematics) [ April 18, 2022 ]
Let a = 635781249. Condition is: 109 | (a101–a) or 109 | a(a100–1). But gcd(a,109) = 1 so 109 | (a100–1).
Factorization: a100–1 = (a–1)(a+1)(a2+1)(a4–a3+a2–a+1)(a4+a3+a2+a+1)(a8–a6+a4–a2+1)(a20–a15+a10–a5+1)(a20+a15+a10+a5+1)(a40–a30+a20–a10+1)
a–1 = 635781248 = 27 x 4967041 (1)
a+1 = 635781250 = 2 x 57 x 13 x 313 (2)
For any number b having the units digit equal to 9 we have:
b2k = 1 (mod 10) and b2k+1 = 9 (mod 10)
So: a4–a3+a2–a+1 = 1–9+1–9+1 = 5 (mod 10) (3)
a20–a15+a10–a5+1 = 1–9+1–9+1 = 5 (mod 10) (4)
2 | (a2+1) (5)
From (1)-(5) we have 29 x 59 = 109 | (a100–1).
Generally 109 | (a100p+1–a) because a100p–1 = (a100)p–1 = (a100–1)(....)
The vertical bar "|" stands for 'divides'
Pari/gp has a simple command for producing the 9 terms of the factorization of our polynomial
(14:00) gp > factor(a^100-1)
%1 =
[ a - 1 1]
[ a + 1 1]
[ a^2 + 1 1]
[ a^4 - a^3 + a^2 - a + 1 1]
[ a^4 + a^3 + a^2 + a + 1 1]
[ a^8 - a^6 + a^4 - a^2 + 1 1]
[ a^20 - a^15 + a^10 - a^5 + 1 1]
[ a^20 + a^15 + a^10 + a^5 + 1 1]
[a^40 - a^30 + a^20 - a^10 + 1 1]
|
759186432 101 =
82260666872235555762250266625924353034740692041723072613225221908129972517410
79368040497793129185854340245930758942254133210108110971390842331027330555511
45540952916667198724287767754930598868574123864483173835155518388996830584546
13989804825083382539061412326421979239699525638449980690283152776976732040942
57670172876623812592321940729721672348124710665628420292270901806076777682020
97119707042032611205871824644392576564139193660812280032933061445605398390813
62055942901999401281725178269911388104228461256806247365431808150705536156893
18074291525522027694579819766996084171946251019573016891903101807872335414382
00201049471880295553020076943765175630219726442008847791105863542328160017318
83759251038778125207733504866110163801274171321479184174034631872273411246535
87680690571780670261116973775768781659632439322592913922927917692091904847243
44882494258519860070773612938144395368838759186432
|
759186432 201 =
89132484842206877224072333243882506481115047313501101593088591184654074856787
63195684432935384031288734506632618449021116516970989054557921092003073207419
78479610779365972342221373501421522475350316784210568722785016071585147887492
02734539633763612017476752173919263236333819514270305324688561049270188451486
21147118809388065383865436743357629844861804969660154563123016123042313614003
62930246401192497775895803344289731467512848459607878351483474766372717072170
72387197272893442098015714115198644477427427325214673723807387888482089247653
77713292922674286121689642433842212615229467646834807727260832188051558076507
09981257282535659403140674107145053077526002195201874023560057448303561661798
61884410043177391932703549065128308458939699325358798388911019573385219675317
44304617123012875316218376972594091512377127286897587775815981743533912623838
56891318749407882925680202903687650146268327404146267989090593999139072008668
13152327959295675141732681913571442322026768520084206924322401284323051403931
18979626641294646900049725069715540043368443224646343909861329258844132645237
00018024140684898981964083443341171876770172664139574056850248865093599257501
52483471350428752707577072001175666443593196701391561839123177816910486810554
86641171033353320729383984411167679719685156850021899792923469802870824357951
91771977135678534646580603614690229469306152174199854050309718399182634706016
16755110706693758601025701391444170431983397789955190084099233749081100187002
32092470774753064256464083708602000228504033289282060520062030789050191507276
39346252346659300692770630426425612810233260919192116983870103183654164035241
86276734604974270732789976436486933032848696626657420385705659400865290003030
23110278498632320836527984228015516860892875165241714612843846337970412777633
93926759186432
In both cases the expansion ends with our ninedigital !!
Here also I detected a pattern as for all exponents +100 (starting with 1) it occurs.
1, 101, 201, 301, ...
|
|
826315794 23 =
12426797981687139976318194833800965760178941008925651967284591535884639168127
69048144289039195619651222534322636314920864225698824936480144264484392524652
8635188413679903582631579460068981211460106226499584
|
|
873264591 83 =
13034837372853334164238093382491785728595445636980606552677673905144344811209
36662942425790599835613708911373168631742552867591811425692124430330075409429
94755619948421750835314736209456882857274065496962124999162871439340633338995
04647924034305980271186771316971847687817508159884016625445308567446163138679
20006235542264658107219655488515060394364853003282248342845474873264591141569
44635942228225266830138874923545164149517423839878166331320624862020348714225
05181805029396362821890131393393223912184424551405029731746354590346537906403
67581873950902768490320199664827709531782965695130366107984725738284643788944
02735317759361314929421354339292024390717560432540358188871423020947904182402
43462672111318591628952881312605495336284911804271
|
|
With 873264591 I found the largest ninedigital with p < 119 !
Topic 5.12 [ March 1, 2015 ]
Nine- & pandigitals equal to the sum of two squares
 Some statistics and curios
Some statistics and curios
This topic is a continuation from wonplate193
Statistics and curios for the ninedigital variation
In total there are 65795 ninedigitals that can be expressed as sums of two squares in 1 or more ways.
This is around 18% of the 9! possible ninedigitals. Here is the distribution list :
(*_1)  28763 28763
(*_2)  25968 25968
(*_3)  1464 1464
(*_4)  7513 7513
(*_5)  55 55
(*_6)  848 848
(*_7)  0 0
(*_8)  901 901
(*_9)  27 27
(*_10)  34 34
(*_11)  0 0
(*_12)  161 161
(*_13)  0 0
(*_14)  0 0
(*_15)  2 469738125 & 879463125 2 469738125 & 879463125
(*_16)  44 44
|
(*_17)  0 0
(*_18)  4 346978125, 647193825, 783961425 & 968417325 4 346978125, 647193825, 783961425 & 968417325
(*_19)  0 0
(*_20)  2 763498125 & 796843125 2 763498125 & 796843125
(*_21)  0 0
(*_22)  0 0
(*_23)  0 0
(*_24)  8 8
(*_25)  0 0
(*_26)  0 0
(*_27)  0 0
(*_28)  0 0
(*_29)  0 0
(*_30)  0 0
(*_31)  0 0
(*_32)  1 439817625 1 439817625
|
In total there are exactly 100 ninedigitals expressible as a sum of two squares whereby
the concatenation of its basenumbers forms a ninedigital (77 in total) or a pandigital (23 in total).
As a coincidence there are also 23 ninedigitals whereby the basenumbers A and B are the same.
They show up on the right side of the table.
One ninedigital stands out from the rest namely 317928645 because it is the
only one that has more than one solution. Beware this is a unique case!
This couple are the first two from an eightfold (*_8) solution for this ninedigital.
Note: this curio was first observed by Peter Kogel already in 2005.
|
317928645 = |
↗
↘ |
25382 + 176492
29432 + 175862
|
Here is the complete list of all the hundred ninedigital solutions.
What is under construction is the list regarding the pandigitals. B.S. Rangaswamy sent me already one example
to wet your appetite. See at the bottom of the table.
| 1 | 175236849 = 34952 + 127682 | | 612859437 = 137492 + 205892 | | 143752968 = 2 * 84782 |
| 2 | 179684325 = 36542 + 128972 | | 618542937 = 136592 + 207842 | | 145897362 = 2 * 85412 |
| 3 | 189237465 = 45362 + 129872 | | 689537412 = 109742 + 238562 | | 162973458 = 2 * 90272 |
| 4 | 197485632 = 53762 + 129842 | | 756928314 = 149672 + 230852 | | 164275938 = 2 * 90632 |
| 5 | 218367945 = 54692 + 137282 | | 783691245 = 185732 + 209462 | | 178945362 = 2 * 94592 |
| 6 | 231649785 = 65282 + 137492 | | 786425193 = 159482 + 230672 | | 183974562 = 2 * 95912 |
| 7 | 234169785 = 76592 + 132482 | | 814593672 = 158942 + 237062 | | 219367458 = 2 * 104732 |
| 8 | 234718965 = 87932 + 125462 | | 817439625 = 137492 + 250682 | | 346581792 = 2 * 131642 |
| 9 | 234971685 = 56792 + 142382 | | 824691537 = 103592 + 267842 | | 423579618 = 2 * 145532 |
| 10 | 237916845 = 89732 + 125462 | | 841769325 = 170582 + 234692 | | 453968712 = 2 * 150662 |
| 11 | 238176549 = 69452 + 137822 | | 867154293 = 169532 + 240782 | | 461593728 = 2 * 151922 |
| 12 | 238971465 = 76592 + 134282 | | 874932516 = 174962 + 238502 | | 497638152 = 2 * 157742 |
| 13 | 243956817 = 27842 + 153692 | | 891746325 = 137852 + 264902 | | 537198642 = 2 * 163892 |
| 14 | 249813657 = 82592 + 134762 | | 912645873 = 164972 + 253082 | | 571963842 = 2 * 169112 |
| 15 | 251649873 = 53672 + 149282 | | 916782345 = 185072 + 239642 | | 618534792 = 2 * 175862 |
| 16 | 256847193 = 49682 + 152372 | | 921847653 = 160982 + 257432 | | 637459218 = 2 * 178532 |
| 17 | 268371954 = 69752 + 148232 | | 925781634 = 143972 + 268052 | | 639174258 = 2 * 178772 |
| 18 | 283974165 = 43592 + 162782 | | 927814653 = 157982 + 260432 | | 654279138 = 2 * 180872 |
| 19 | 286753194 = 82952 + 147632 | | 934687125 = 143702 + 269852 | | 654713298 = 2 * 180932 |
| 20 | 312897645 = 89342 + 152672 | | 943725186 = 187052 + 243692 | | 765421938 = 2 * 195632 |
| 21 | 317928645 = 25382 + 176492 = 29432 + 175862 | | 948571236 = 136802 + 275942 | | 913524768 = 2 * 213722 |
| 22 | 326785149 = 49652 + 173822 | | 972354861 = 174692 + 258302 | | 943256178 = 2 * 217172 |
| 23 | 328459617 = 54362 + 172892 | | 973416285 = 174062 + 258932 | | 958431762 = 2 * 218912 |
| 24 | 341978265 = 64592 + 173282 |
| 25 | 345172689 = 87452 + 163922 |
| 26 | 346297185 = 79532 + 168242 |
| 27 | 362794185 = 54962 + 182372 |
| 28 | 365984721 = 24362 + 189752 |
| 29 | 368529417 = 53762 + 184292 |
| 30 | 369471825 = 59642 + 182732 |
| 31 | 374921865 = 83522 + 174692 |
| 32 | 378129645 = 83492 + 175622 |
| 33 | 385267914 = 23672 + 194852 |
| 34 | 413629578 = 64532 + 192872 |
| 35 | 435869712 = 78242 + 193562 |
| 36 | 436521978 = 96272 + 185432 |
| 37 | 478192653 = 46982 + 213572 |
| 38 | 481379265 = 48572 + 213962 |
| 39 | 489731265 = 56972 + 213842 |
| 40 | 497163825 = 48962 + 217532 |
| 41 | 497231865 = 59762 + 214832 |
| 42 | 514926873 = 57632 + 219482 |
| 43 | 523687194 = 63452 + 219872 |
| 44 | 523861794 = 78632 + 214952 |
| 45 | 532978641 = 87962 + 213452 |
| 46 | 592876413 = 61982 + 235472 |
| 47 | 598314762 = 64712 + 235892 |
| 48 | 613259874 = 18752 + 246932 |
| 49 | 613478925 = 74582 + 236192 |
| 50 | 614829357 = 78692 + 235142 |
| 51 | 619423785 = 15962 + 248372 |
| 52 | 631548297 = 87962 + 235412 |
| 53 | 635127849 = 91682 + 234752 |
| 54 | 639218457 = 73562 + 241892 |
| 55 | 648912537 = 38642 + 251792 |
| 56 | 651429378 = 68132 + 245972 |
| 57 | 674921853 = 41972 + 256382 |
| 58 | 682143597 = 61892 + 253742 |
| 59 | 694725138 = 96872 + 245132 |
| 60 | 712839546 = 97352 + 248612 |
| 61 | 726389145 = 89762 + 254132 |
| 62 | 726439185 = 71642 + 259832 |
| 63 | 729563481 = 39842 + 267152 |
| 64 | 758394621 = 43952 + 271862 |
| 65 | 789631245 = 97412 + 263582 |
| 66 | 812596473 = 56132 + 279482 |
| 67 | 817453962 = 65492 + 278312 |
| 68 | 823415697 = 35162 + 284792 |
| 69 | 825697314 = 39152 + 284672 |
| 70 | 839147625 = 91562 + 274832 |
| 71 | 846352197 = 73592 + 281462 |
| 72 | 865972341 = 38462 + 291752 |
| 73 | 872156394 = 16352 + 294872 |
| 74 | 914367285 = 64712 + 295382 |
| 75 | 931427586 = 68312 + 297452 |
| 76 | 934816725 = 74312 + 296582 |
| 77 | 951246738 = 85172 + 296432 |
Another ninedigital that stands out from the rest is 934167285 because it is the only
one that can be written as a sum of two squares in two different ways such that both
their basenumbers forms a ninedigital when multiplied together.
A nice unique case!
|
934167285 = |
↗
↘ |
95132 + 290462 and 9513 * 29046 = 276314598
206012 + 225782 and 20601 * 22578 = 465129378
|
|
In total there are 219 ninedigitals expressible in this way.
The smallest is 248635917 = 106142 + 116612 and 10614 * 11661 = 123769854
The largest is 987431562 = 215192 + 228992 and 21519 * 22899 = 492763581
Statistics and curios for the pandigital variation
In total there are 568801 pandigitals that can be expressed as sums of two squares in 1 or more ways.
This is around 17,416 % of the 9*9! possible pandigitals. Here is the distribution list :
(*_1) (23112)1 + (23193)2 + (23072)3 + (22132)4 + (24904)5 + (21085)6 + (22492)7 + (21296)8 + (20600)9  ( 201886 )tot ( 201886 )tot
(*_2) (26329)1 + (26858)2 + (26881)3 + (25208)4 + (25865)5 + (24452)6 + (26628)7 + (24705)8 + (24742)9  ( 231668 )tot ( 231668 )tot
(*_3) (1840)1 + (919)2 + (1592)3 + (1372)4 + (511)5 + (1434)6 + (1526)7 + (1324)8 + (1471)9  ( 11989 )tot ( 11989 )tot
(*_4) (10254)1 + (10559)2 + (11129)3 + (10170)4 + (8929)5 + (9983)6 + (11204)7 + (10259)8 + (10737)9  ( 93224 )tot ( 93224 )tot
(*_5) (60)1 + (0)2 + (110)3 + (116)4 + (5)5 + (57)6 + (105)7 + (96)8 + (107)9  ( 656 )tot ( 656 )tot
(*_6) (1408)1 + (740)2 + (1164)3 + (1127)4 + (377)5 + (1185)6 + (1257)7 + (1081)8 + (1156)9  ( 9495 )tot ( 9495 )tot
(*_7) (5)1 + (0)2 + (7)3 + (7)4 + (0)5 + (1)6 + (5)7 + (5)8 + (4)9  ( 34 )tot ( 34 )tot
(*_8) (1601)1 + (1606)2 + (1864)3 + (1748)4 + (1197)5 + (1739)6 + (2088)7 + (1915)8 + (1992)9  ( 15750 )tot ( 15750 )tot
(*_9) (32)1 + (19)2 + (25)3 + (17)4 + (5)5 + (23)6 + (30)7 + (29)8 + (25)9  ( 205 )tot ( 205 )tot
(*_10) (30)1 + (2)2 + (42)3 + (90)4 + (0)5 + (40)6 + (82)7 + (53)8 + (72)9  ( 411 )tot ( 411 )tot
(*_11) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_12) (251)1 + (133)2 + (281)3 + (266)4 + (73)5 + (270)6 + (297)7 + (290)8 + (294)9  ( 2155 )tot ( 2155 )tot
(*_13) (1)1 + (0)2 + (0)3 + (1)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 2 )tot ( 2 )tot
(*_14) (0)1 + (0)2 + (1)3 + (4)4 + (0)5 + (4)6 + (3)7 + (1)8 + (7)9  ( 20 )tot ( 20 )tot
(*_15) (2)1 + (0)2 + (4)3 + (6)4 + (0)5 + (0)6 + (5)7 + (1)8 + (2)9  ( 20 )tot ( 20 )tot
(*_16) (88)1 + (71)2 + (111)3 + (114)4 + (49)5 + (128)6 + (142)7 + (156)8 + (153)9  ( 1012 )tot ( 1012 )tot
(*_17) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_18) (9)1 + (3)2 + (11)3 + (14)4 + (2)5 + (7)6 + (9)7 + (14)8 + (10)9  ( 79 )tot ( 79 )tot
(*_19) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_20) (1)1 + (0)2 + (4)3 + (6)4 + (0)5 + (7)6 + (17)7 + (3)8 + (8)9  ( 46 )tot ( 46 )tot
(*_21) (1)1 + (0)2 + (1)3 + (0)4 + (0)5 + (0)6 + (1)7 + (0)8 + (0)9  ( 3 )tot ( 3 )tot
(*_22) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_23) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_24) (11)1 + (9)2 + (14)3 + (12)4 + (3)5 + (12)6 + (23)7 + (8)8 + (22)9  ( 114 )tot ( 114 )tot
(*_25) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_26) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_27) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_28) (0)1 + (0)2 + (0)3 + (1)4 + (0)5 + (0)6 + (0)7 + (1)8 + (1)9  ( 3 )tot ( 3 )tot
(*_29) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_30) (0)1 + (0)2 + (2)3 + (2)4 + (0)5 + (0)6 + (1)7 + (1)8 + (0)9  ( 6 )tot ( 6 )tot
(*_31) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_32) (2)1 + (0)2 + (3)3 + (1)4 + (0)5 + (3)6 + (2)7 + (2)8 + (3)9  ( 16 )tot ( 16 )tot
(*_33) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_34) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_35) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_36) (0)1 + (0)2 + (1)3 + (0)4 + (0)5 + (1)6 + (1)7 + (0)8 + (2)9  ( 5 )tot 3049186725, 6137904825, 7261938450, 9132768450 & 9702436185 ( 5 )tot 3049186725, 6137904825, 7261938450, 9132768450 & 9702436185
(*_37) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_38) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_39) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_40) (0)1 + (0)2 + (0)3 + (1)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 1 )tot 4398176250 ( 1 )tot 4398176250
(*_41) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_42) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_43) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_44) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_45) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_46) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_47) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (0)7 + (0)8 + (0)9  ( 0 )tot ( 0 )tot
(*_48) (0)1 + (0)2 + (0)3 + (0)4 + (0)5 + (0)6 + (1)7 + (0)8 + (0)9  ( 1 )tot 7316984025 ( 1 )tot 7316984025
(*_subt) (65037)1 + (64112)2 + (66319)3 + (62415)4 + (61920)5 + (60431)6 + (65919)7 + (61240)8 + (61408)9  ( 568801 )total ( 568801 )total
|
| 1 | 1023458976 = 194762 + 253802 | |
1 | 1024397685 = 57692 + 314822 |
| 2 | 1024537896 = 193862 + 254702 | |
2 | 1063789245 = 78422 + 316592 |
| 3 | 1024736985 = 165392 + 274082 | |
3 | 1073982645 = 89462 + 315272 |
| 4 | 1032768549 = 146702 + 285932 | |
4 | 1074893265 = 15692 + 327482 |
| 5 | 1038249657 = 185042 + 263792 | |
5 | 1236785940 = 51962 + 347822 |
| 6 | 1038259476 = 198602 + 253742 | |
6 | 1237694085 = 56822 + 347192 |
| 7 | 1058267349 = 184502 + 267932 | |
7 | 1258047369 = 67952 + 348122 |
| 8 | 1063275498 = 159032 + 284672 | |
8 | 1270365489 = 81752 + 346922 |
| 9 | 1073982645 = 198542 + 260732 | |
9 | 1294037685 = 92582 + 347612 |
| 10 | 1075348296 = 145862 + 293702 | |
10 | 1324958760 = 71942 + 356822 |
| 11 | ° = ° + ° | |
11 | ° = ° + ° |
| 12 | ° = ° + ° | |
12 | ° = ° + ° |
One lovely pandigital already popped up on my screen 1073982645
It combines in an elegant way the two numberformats i.e. ninedigital and pandigital !
This couple are the middle two from a fourfold (*_4) solution for this pandigital.
|
1073982645 = |
↗
↘ |
89462 + 315272
198542 + 260732
|
Then three more pandigitals with double solutions popped up later on !
They are fully pandigital solutions throughout. Enjoy them!
|
7095281346 = |
↗
↘ |
207452 + 816392
398612 + 742052
|
|
7125094386 = |
↗
↘ |
312692 + 784052
497312 + 682052
|
|
7465102389 = |
↗
↘ |
369422 + 781052
469832 + 725102
|
Two pandigitals that stand out from the rest are 5921803476 and 8097452136 because
they are the only ones that can be written as a sum of two squares such that both their
basenumbers form a pandigital when concatenated as well as when multiplied together.
A nice couplet !
|
5921803476 = 357902 + 681242 and 35790 * 68124 = 2438157960 |
|
|
8097452136 = 251702 + 863942 and 25170 * 86394 = 2174536980 |
|
While tracing for long(er) chains of pandigitals I stumbled across the following unique and
unexpectedly double expression. A thing of beauty !
Note that A and B are in descending order here. I didn't find a case whereby A and B are ascending.
|
7983056241 = 75129 2 + 48360 2
and the concatenation of A | B gives us
7512948360 = 75306 2 + 42918 2
a similar all_pandigital expression !
|
|
Can you find longer chains of pandigital expressions using perhaps other operations than concatenation ?
More subcategories
All the pandigitals (41) equal to 2 x A2 are A =
22887, 23124, 24957, 25941, 26409, 26733, 27276, 29685, 31389, 35367,
39036, 39147, 39432, 39702, 40293, 41997, 42843, 43059, 44922, 45258,
45624, 46464, 49059, 50889, 53568, 54354, 57321, 59268, 59727, 60984,
61098, 61611, 61866, 62634, 65436, 68823, 68982, 69087, 69696, 69732,
69798.
Note that two of them (see underlined) are palindromic !
All the pandigitals (46) equal to (A)2 + (AReversed)2 are A (smallest) =
10716, 12804, 14496, 14967, 16053, 18126, 18528, 19317, 20493, 21423, 21792,
22839, 23205, 23286, 23544, 24267, 26058, 27324, 28557, 28563, 30597, 32325,
32838, 33105, 37824, 41676, 41718, 41736, 42378, 43497, 43725, 45018, 46464,
47217, 49245, 49305, 51327, 52866, 53436, 54456, 55296, 56247, 60927, 63666,
67137, 69696.
Note that the same two palindromes appear again !
The most beautiful one however seems to me the next one
8493716052 = 636662 + 666362
When the number of the beast gets involved...
There are 2187 pandigitals that can be expressed as (A)2 + (BAnagram of A)2
The reversals of above paragraph are evidently included in this total.
0001 1023849765 = 223862 + 228632 smallest
0002 1027935648 = 223082 + 230282 second
0003 1027968345 = 176282 + 267812 third
- - -
0666 3921846057 = 107162 + 617012 indexed by the number of the beast yields a reversal
1666 7914563208 = 260582 + 850622 indexed by a near number of the beast yields also a reversal
- - -
2185 9864025713 = 339722 + 933272 third last
2186 9872350146 = 154892 + 981452 penultimate
2187 9876135240 = 657422 + 745262 largest
The following is special as the five lowest and five highest digits of the pandigital are nicely separated
1082 56789_04132 = 507542 + 557042 curio
There are four pandigitals whose second half is also an anagram of A or B
0371 26904_57813 = 358172 + 375182 curio
1062 54903_21768 = 187622 + 716822 curio
1175 60294_17538 = 518372 + 578132 curio
1865 85764_92130 = 209312 + 902132 curio
These two solutions are also noteworthy
0957 5047168932 = 246662 + 666242 curio with number of the beast
1731 8140532769 = 158882 + 888152 curio not with number of the beast but same structure
Topic 5.11 [ April 27, 2014 ]
Order out of chaos using the ninedigits
Numberphile has released a video file that relates to the ninedigits.
Near the end of the video the zero comes in as well!
https://www.youtube.com/watch?v=CwIAfkuXc5A&feature=em-uploademail
And here is a video explaining the mysterious math from above
which is in fact the Erdös-Szekeres theorem.
https://www.youtube.com/watch?v=LBPj8E1JKaQ&feature=em-uploademail
Topic 5.10 [ December 15, 2013 ]
Nearing the end of the year 2013
There is a
unique ninedigital number that when divided by the year 2013 delivers a palindrome.
Ain't that nice!
127495368 = 2013 * 63336
Who likes to do this exercise for the coming years 2014, 2015, ...
And what about the pandigital version of this topic ?
Topic 5.9 [ January 1, 2013 ]
The ninedigital primes version of WONplate 181
The following ninedigital numbers are all (probable (3-PRP!)) prime.
Note that the 5-digit displacements are also prime !
1325! + 87649
1462! + 59387
1475! + 96823
1547! + 68239
1685! + 29437
2351! + 74869
2354! + 86197
2468! + 75193
2486! + 15973
2615! + 84793
2876! + 15493
3218! + 45697
3845! + 76129
4618! + 32579
4895! + 76213
4981! + 62753
8153! + 72649
8573! + 41269
9625! + 34781
9824! + 61357
|
1438! - 57269
1478! - 52369
1486! - 59273
1576! - 28493
1849! - 67523
2471! - 63589
2536! - 84179
3469! - 28751
4285! - 71963
4562! - 93871
4691! - 52837
5239! - 16487
5417! - 86923
5462! - 98317
5743! - 68219
5749! - 26183
7948! - 23561
7982! - 45361
8123! - 47569
9836! - 25147
|
Topic 5.8 [ December 30, 2010 ]
From a posting to [SeqFan]
by Eric Angelini
"As an afterthought, here's one I like (because of
the symmetry in the operations) that was appropriate
for the countdown on Friday night {
can you find out the exact year? }:
10 + 9 * 8 * 7 / 6 * 5 * 4 + 321
Happy New Year! "
Topic 5.7 [ April 2008 ]
Fractions using the same digits as their decimal representation
A webpage by Christian Boyer
An example using all the nine digits from
http://www.christianboyer.com/fractiondigits/ is
124983 / 576 = 216.984375
The above link came from a reply in the SeqFan mailing list where
Alexander R. Povolotsky's topic was about approximating Pi
using just nine- and pandigitals. Here is his *best* combination !
689725314(0) / 219546387(0) = 3.141592642...
Alexander R. Povolotsky [ October 8, 2022 ] writes
Since then the better approximations were found per
Using each number (1-9 EXACTLY ONCE) can you make 2 distinct 9 digits numbers,
so the quotient of the two numbers is as close to Pi as possible?
429751836 / 136794258 = 3.14159265369164852899... (pi + 1.01855e-10)
467895213 / 148935672 = 3.14159265350479621759... (pi - 8.49969e-11)
Pi = 3.1415926535897932384626433832795028842
I conjecture that the higher the pandigital number base then the better and better Pi approximations
can be found and that in the base where n=infinity the actual Pi number could be achieved...
Someone with good computer programming skills perhaps could check whether my conjecture is true or not.
|
Topic 5.6 [ March 31, 2008 ]
Blending palindromes with nine- & pandigitals using multiplication by 9
by B.S. Rangaswamy
This topic is a continuation from
wonplate 173.
Pandigitals (Kmil = 1000 million)  total = 559
total = 559
Palindrome Pandigital
P9 P9 * 9
Palindrome Ninedigital
P8 P8 * 9 | Palindrome Pandigital
P9 P9 * 9
Palindrome Ninedigital
P8 P8 * 9 | Palindrome Pandigital
P9 P9 * 9
Palindrome Ninedigital
P8 P8 * 9 | Palindrome Pandigital
P9 P9 * 9
Palindrome Ninedigital
P8 P8 * 9 |
|---|
1 Kmil  # 81
2 Kmil # 81
2 Kmil  # 46 # 46
134050431 1206453879
134060431 1206543879
136717631 1230458679
136727631 1230548679
137606731 1238460579
137626731 1238640579
137818731 1240368579
137848731 1240638579
138929831 1250368479
138959831 1250638479
139828931 1258460379
139848931 1258640379
143050341 1287453069
143060341 1287543069
145030541 1305274869
145080541 1305724869
145272541 1307452869
145282541 1307542869
146717641 1320458769
146727641 1320548769
148919841 1340278569
148969841 1340728569
152676251 1374086259
152898251 1376084259
154030451 1386274059
154080451 1386724059
156252651 1406273859
156303651 1406732859
156373651 1407362859
157818751 1420368759
157848751 1420638759
158707851 1428370659
158747851 1428730659
158919851 1430278659
158969851 1430728659
167030761 1503276849
167080761 1503726849
167363761 1506273849
167414761 1506732849
167484761 1507362849
168929861 1520368749
168959861 1520638749
169818961 1528370649
169858961 1528730649
174898471 1574086239
176030671 1584276039
176080671 1584726039
176252671 1586274039
178050871 1602457839
178060871 1602547839
178252871 1604275839
178363871 1605274839
182565281 1643087529
183676381 1653087429
187050781 1683457029
187060781 1683547029
187303781 1685734029
187494781 1687453029
189272981 1703456829
189282981 1703546829
189373981 1704365829
189484981 1705364829
189515981 1705643829
215030512 1935274608
215080512 1935724608
215272512 1937452608
215282512 1937542608
216252612 1946273508
216303612 1946732508
217030712 1953276408
217080712 1953726408
217414712 1956732408
217484712 1957362408
218050812 1962457308
218060812 1962547308
218363812 1965274308
219272912 1973456208
219282912 1973546208
219373912 1974365208
219484912 1975364208
219515912 1975643208
224050422 2016453798
224060422 2016543798
225717522 2031457698
225727522 2031547698
226404622 2037641598
226818622 2041367598
226848622 2041637598
227959722 2051637498
240545042 2164905378
240656042 2165904378
255717552 2301457968
255727552 2301547968
264010462 2376094158
264404462 2379640158
266818662 2401367958
266848662 2401637958
268121862 2413096758
268454862 2416093758
277929772 2501367948
277959772 2501637948
279232972 2513096748
279565972 2516093748
286010682 2574096138
286232682 2576094138
286606682 2579460138
286626682 2579640138
315010513 2835094617
315494513 [Obs] 2839450617
315595513 2840359617
315989513 2843905617
316595613 2849360517
317010713 2853096417
318232813 2864095317
318343813 2865094317
326020623 2934185607
326090623 2934815607
326131623 2935184607
326494623 2938451607
327020723 2943186507
327090723 2943816507
327353723 2946183507
327595723 2948361507
328464823 2956183407
329050923 2961458307
329060923 2961548307
329464923 2965184307
|
3 Kmil  # 74
4 Kmil # 74
4 Kmil  # 90 # 90
336020633 3024185697
336090633 3024815697
336131633 3025184697
336494633 3028451697
341050143 3069451287
341060143 3069541287
344717443 3102456987
344727443 3102546987
347121743 3124095687
347232743 3125094687
360121063 3241089567
360212063 3241908567
360989063 3248901567
361202163 3250819467
361232163 3251089467
361323163 3251908467
364505463 3280549167
364989463 3284905167
365101563 3285914067
365494563 3289451067
365717563 3291458067
365727563 3291548067
378101873 3402916857
378545873 3406912857
389212983 3502916847
389656983 3506912847
412050214 3708451926
412060214 3708541926
412676214 3714085926
412787214 3715084926
413272314 3719450826
413282314 3719540826
416454614 3748091526
416545614 3748910526
416575614 3749180526
417565714 3758091426
417656714 3758910426
417686714 3759180426
420545024 3784905216
420656024 3785904216
422050224 3798452016
422060224 3798542016
423050324 3807452916
423060324 3807542916
425010524 3825094716
425494524 3829450716
427454724 3847092516
427696724 3849270516
428010824 3852097416
428565824 3857092416
431050134 3879451206
431060134 3879541206
432505234 3892547106
432747234 3894725106
432808234 3895274106
432858234 3895724106
435030534 3915274806
435080534 3915724806
435272534 3917452806
435282534 3917542806
435717534 3921457806
435727534 3921547806
436020634 3924185706
436090634 3924815706
436131634 3925184706
436494634 3928451706
438020834 3942187506
438090834 3942817506
438575834 3947182506
438696834 3948271506
439030934 3951278406
439080934 3951728406
439131934 3952187406
439686934 3957182406
445919544 4013275896
446202644 4015823796
448020844 4032187596
448090844 4032817596
448575844 4037182596
448646844 4037821596
448696844 4038271596
451030154 4059271386
451080154 4059721386
452373254 4071359286
452393254 4071539286
455919554 4103275986
455969554 4103725986
459121954 4132097586
459676954 4137092586
462010264 4158092376
462202264 4159820376
467101764 4203915876
480212084 4321908756
480989084 4328901756
485676584 4371089256
485767584 4371908256
486454684 4378092156
486646684 4379820156
486989684 4382907156
487545784 4387912056
487919784 4391278056
487969784 4391728056
512030215 4608271935
512080215 4608721935
512303215 4610728935
513010315 4617092835
513252315 4619270835
513353315 4620179835
513545315 4621907835
514232415 4628091735
514323415 4628910735
514353415 4629180735
519010915 4671098235
519787915 4678091235
519878915 4678910235
521454125 4693087125
521898125 4697083125
523181325 4708631925
523404325 4710638925
523676325 4713086925
524010425 4716093825
524373425 4719360825
526454625 4738091625
526545625 4738910625
526575625 4739180625
529010925 4761098325
529787925 4768091325
529878925 4768910325
531545135 4783906215
531878135 4786903215
533151335 4798362015
533181335 4798632015
534030435 4806273915
534080435 4806723915
534151435 4807362915
534181435 4807632915
536232635 4826093715
536595635 4829360715
536696635 4830269715
536989635 4832906715
537454735 4837092615
537696735 4839270615
541030145 4869271305
541080145 4869721305
541252145 4871269305
541292145 4871629305
542151245 4879361205
542181245 4879631205
543626345 4892637105
543747345 4893726105
546252645 4916273805
546303645 4916732805
546373645 4917362805
546818645 4921367805
546848645 4921637805
547020745 4923186705
547090745 4923816705
547353745 4926183705
547595745 4928361705
548020845 4932187605
548090845 4932817605
548575845 4937182605
548646845 4937821605
548696845 4938271605
|
5 Kmil  # 64
6 Kmil # 64
6 Kmil  # 78 # 78
623020326 5607182934
623090326 5607812934
623141326 5608271934
623191326 5608721934
623414326 5610728934
623565326 5612087934
624121426 5617092834
624363426 5619270834
624464426 5620179834
624656426 5621907834
625343526 5628091734
625434526 5628910734
625464526 5629180734
630121036 5671089324
630212036 5671908324
630989036 5678901324
632565236 5693087124
633020336 5697183024
633090336 5697813024
634020436 5706183924
634090436 5706813924
634262436 5708361924
634292436 5708631924
634515436 5710638924
634787436 5713086924
635121536 5716093824
635484536 5719360824
637565736 5738091624
637656736 5738910624
637686736 5739180624
642656246 5783906214
642989246 5786903214
644262446 5798362014
644292446 5798632014
645141546 5806273914
645191546 5806723914
645262546 5807362914
645292546 5807632914
647010746 5823096714
647343746 5826093714
648010846 5832097614
648565846 5837092614
652141256 5869271304
652191256 5869721304
652363256 5871269304
653262356 5879361204
653292356 5879631204
654707456 5892367104
654737456 5892637104
654808456 5893276104
654858456 5893726104
657030756 5913276804
657080756 5913726804
657363756 5916273804
657414756 5916732804
657484756 5917362804
657929756 5921367804
657959756 5921637804
658131856 5923186704
658464856 5926183704
659030956 5931278604
659080956 5931728604
659131956 5932187604
659686956 5937182604
668202866 6013825794
668424866 6015823794
671030176 6039271584
671080176 6039721584
673101376 6057912384
673252376 6059271384
674595476 6071359284
682010286 6138092574
682202286 6139820574
684232486 6158092374
684424486 6159820374
689323986 6203915874
689545986 6205913874
712030217 6408271953
712080217 6408721953
712303217 6410728953
712454217 6412087953
713010317 6417092853
713252317 6419270853
713353317 6420179853
713545317 6421907853
714232417 6428091753
714323417 6428910753
714353417 6429180753
719010917 6471098253
719878917 6478910253
723020327 6507182943
723090327 6507812943
723141327 6508271943
723191327 6508721943
723414327 6510728943
723565327 6512087943
724121427 6517092843
724363427 6519270843
724464427 6520179843
724656427 6521907843
725343527 6528091743
725434527 6528910743
725464527 6529180743
745020547 6705184923
745090547 6705814923
745383547 6708451923
745393547 6708541923
745606547 6710458923
745616547 6710548923
746010647 6714095823
746121647 6715094823
749010947 6741098523
749787947 6748091523
749878947 6748910523
753878357 6784905213
753989357 6785904213
755383557 6798452013
755393557 6798542013
756030657 6804275913
756080657 6804725913
756141657 6805274913
756191657 6805724913
756383657 6807452913
756393657 6807542913
758232857 6824095713
758343857 6825094713
761030167 6849271503
761080167 6849721503
762141267 6859271403
762191267 6859721403
764383467 6879451203
764393467 6879541203
765828567 6892457103
765838567 6892547103
768050867 6912457803
768060867 6912547803
768252867 6914275803
768363867 6915274803
769050967 6921458703
769060967 6921548703
769353967 6924185703
769464967 6925184703
|
7 Kmil  # 69
8 Kmil # 69
8 Kmil  # 57 # 57
781050187 7029451683
781060187 7029541683
783474387 7051269483
785101587 7065914283
785494587 7069451283
812050218 7308451962
812060218 7308541962
812676218 7314085962
812787218 7315084962
816454618 7348091562
816575618 7349180562
817565718 7358091462
817656718 7358910462
821565128 7394086152
821787128 7396084152
823151328 7408361952
823181328 7408631952
824010428 7416093852
824373428 7419360852
826454628 7438091652
826545628 7438910652
826575628 7439180652
829010928 7461098352
829787928 7468091352
829878928 7468910352
834020438 7506183942
834090438 7506813942
834262438 7508361942
834292438 7508631942
834515438 7510638942
834787438 7513086942
835121538 7516093842
835484538 7519360842
837565738 7538091642
837656738 7538910642
837686738 7539180642
840121048 7561089432
840212048 7561908432
840989048 7568901432
843787348 7594086132
844020448 7596184032
844090448 7596814032
845020548 7605184932
845090548 7605814932
845383548 7608451932
845393548 7608541932
845606548 7610458932
845616548 7610548932
846010648 7614095832
846121648 7615094832
849010948 7641098532
849787948 7648091532
849878948 7648910532
867050768 7803456912
867060768 7803546912
867151768 7804365912
867181768 7804635912
867383768 7806453912
867393768 7806543912
871050178 7839451602
871060178 7839541602
871262178 7841359602
873262378 7859361402
873292378 7859631402
874383478 7869451302
874393478 7869541302
879272978 7913456802
879282978 7913546802
879515978 7915643802
915010519 8235094671
915595519 8240359671
915989519 8243905671
916595619 8249360571
917010719 8253096471
917343719 8256093471
918232819 8264095371
918343819 8265094371
923050329 8307452961
923060329 8307542961
925010529 8325094761
925494529 8329450761
927454729 8347092561
927696729 8349270561
928010829 8352097461
928565829 8357092461
934030439 8406273951
934080439 8406723951
934151439 8407362951
934181439 8407632951
936232639 8426093751
936595639 8429360751
936696639 8430269751
936989639 8432906751
937454739 8437092651
937696739 8439270651
945141549 8506273941
945191549 8506723941
945262549 8507362941
945292549 8507632941
947010749 8523096741
947343749 8526093741
948010849 8532097641
948565849 8537092641
951434159 8562907431
951989159 8567902431
955141559 8596274031
955191559 8596724031
956030659 8604275931
956080659 8604725931
956141659 8605274931
956383659 8607452931
956393659 8607542931
958232859 8624095731
958343859 8625094731
963878369 8674905321
963989369 8675904321
966383669 8697453021
966393669 8697543021
967050769 8703456921
967060769 8703546921
967151769 8704365921
967181769 8704635921
967262769 8705364921
967292769 8705634921
967383769 8706453921
967393769 8706543921
|
[ June 14, 2014 ]
Observation 1 by Heine Wanderlust (email)
315494513 (a prime by the way) * 9 = the pandigital 2839450617.
But multiply by 18 and you get a pandigital with a nice permutation: 5678901234.
Also in both these pandigitals the differences between each
successive digit creates a palindrome: 656515656, 111191111
[ September 15, 2014 ]
Observation 2 by Heine Wanderlust (email)
Following on from my June 14 2014 post, I've found another Rangaswamy palindrome
yielding a pandigital when multiplied by 18 as well as by 9 :
548696845 * 18 = 9876543210
548696845 * 9 = 4938271605
This type of result, whereby the "countdown" pandigital in a base b can be divided by 2(b–1)
to get a palindrome, occurs in at least two other number bases:
base 8 where 76543210 / 16 = 4364634, and in base 6 where 543210 / 14 = 32423.
Topic 5.5 [ January 22, 2006 ]
Pandigital... throughout
A unique construction : start with multiplying these two
5-digit factors which taken together form a pandigital number :
equals
as you can see the result of the multiplication is pandigital as well.
And now let us take the square of this pandigital 34108562972
... an order_2 pandigital emerges since all the digits from 0 to 9
occur exactly two times !
Discover more of these gems at  wonplate 167 !
wonplate 167 !
Topic 5.4 [ October 26, 2005 ]
From Palindromic Squares to Pandigitals
264 is a very interesting number since it is the 12
th basenumber of a
palindromic square.
The square itself is this nice palindrome
69696.
Note the presence of the number of the Beast !
69696 .
Did you know that when we power up 264 with two exponents and add them up
that we arrive at a pandigital number... in two different ways !
2643 + 2644 = 4875932160
2644 + 2644 = 9715064832 |
|---|
The second equation can be written as a palindromic expression itself using
69696 squared and then doubled
2 * 69696 ^ 2
(There exists another 5-digit palindrome with this property. Can you discover it ?)
- B.S. Rangaswamy [ August 11, 2006 ] was enthused by this presentation
- and found the following solutions :
232322 * 8 = 4317806592 = 464642 * 2
- 232322 * 18 = 9715064832 = 696962 * 2
423242 * 4 = 7165283904 |
|---|
One can play along with other than our 264 number namely 2016.
I found the next equation of some interest.
| 20162 + 20163 = 8197604352 |
|---|
Or the next one with two consecutive integers
Is there more to discover ?
Yes, see Claudio Meller's contribution at WONplate 183
Topic 5.3 [ October 2005 ]
Figure this out : 4-1-4
 It is a four digit number multiplied by a one digit number to equal another four digit number
It is a four digit number multiplied by a one digit number to equal another four digit number
and only the nine digits from 1 to 9 can be used once ?
Two solutions to this 9-digit problem can be found.
1738 * 4 = 6952
1963 * 4 = 7852 |
|---|
Topic 5.2 [ October 2006 ]
Figure this out : 4-1-5
 It is a four digit number multiplied by a one digit number to equal a five digit number
It is a four digit number multiplied by a one digit number to equal a five digit number
and only the ten digits from 0 to 9 can be used once ?
Thirteen solutions to this pandigital problem can be found.
3094 * 7 = 21658
3907 * 4 = 15628
4093 * 7 = 28651
5694 * 3 = 17082
5817 * 6 = 34902
6819 * 3 = 20457
6918 * 3 = 20754
7039 * 4 = 28156
8169 * 3 = 24507
9127 * 4 = 36508
9168 * 3 = 27504
9304 * 7 = 65128
9403 * 7 = 65821 |
|---|
Topic 5.1 [ September 4, 2005 ]
Generating Pandigitals from Palindromes through Fibonacci iteration
by B.S. Rangaswamy
" I got inspired by your presentation of the derivation of 68 ninedigit numbers (with all numerals from 1 to 9)
from palindromes through Fibonacci iteration. I have developed it further by arriving at a dozen 10 digit numbers
(with all numerals from 0 to 9) from 2 to 10 digit palindromes. Some of the 10 digit numbers arrived at
together with their mother palindromes are :
75257  9135748206 9135748206
799997  2067193845 2067193845
8055508  4913860257 4913860257
42944924  2361970854 2361970854 |
It is interesting to note that 6300036 leads to pandigital 1467908532, which matches identically
with each stage of iteration of 630036 to 146798532. I came across another curio as well :
630036  146798532 146798532
6300036  1467908532 1467908532
9530359  123894675 123894675
95300359 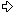 1238904675 1238904675 |
Following closely resembling palindromes lead to closely matching pandigitals :
592070295  2960351478 2960351478
952070259  4760351298 4760351298 |
This task began at my son's residence in Florida US and was completed at Bangalore India.
I was thrilled at the discovery of each of these pandigitals.
I am grateful to you for your encouragement and guidance in this venture.
B.S.Rangaswamy "
In total there are 117 palindromes that yield pandigital numbers
The smallest one is 75257 and the largest one is 4376006734 ¬
1. Typical generation of pandigitals (10 digits) from palindromes through Fibonacci iteration
1
75257
75258
150515
225773
376288
602061
978349
1580410
2558759
4139169
6697928
10837097
17535025
28372122
45907147
74279269
120186416
194465685
314652101
509117786
823769887
1332887673
2156657560
3489545233
5646202793
9135748026 |
1
799997
799998
1599995
2399993
3999988
6399981
10399969
16799950
27199919
43999869
71199788
115199657
186399445
301599102
487998547
789597649
1277596196
2067193845 |
1
6431346
6431347
12862693
19294040
32156733
51450773
83607506
135058279
218665785
353724064
572389849
926113913
1498503762 |
1
408676804
408676805
817353609
1226030414
2043384023
3269414437
5312798460 |
1
561262165
561262166
1122524331
1683786497
2806310828
4490097325
7296408153 |
1
760474067
760474068
1520948135
2281422203
3802370338
6083792541 |
1
93811839
93811840
187623679
281435519
469059198
750494717
1219553915
1970048632
3189602547 |
1
1206776021
1206776022
2413552043
3620328065
6033880108
9654208173 |
1
3067447603
3067447604
6134895207 |
1
4068228604
4068228605
8136457209 |
117
in total |
2. Above are 117 palindromes in ascending order, leading to pandigitals (10 digits)
75257
799997
2877782
4364634
4689864
5068605
6300036
6431346
6881886
8055508
15844851
42944924
54777745
93811839
95300359 |
146353641
177858771
185121581
185222581
187333781
207313702
238242832
245363542
295747592
310717013
314878413
324151423
348616843
350878053
354010453 |
358070853
370464073
370797073
390474093
394070493
395313593
395727593
407525704
408676804
460363064
473303374
475686574
506939605
527121725
527454725 |
530878035
536454635
547252745
561262165
590272095
592070295
629171926
642676246
655191556
695525596
740838047
760474067
782484287
841303148
914272419 |
950272059
952070259
1089229801
1097337901
1098228901
1206776021
1289009821
1295335921
1298008921
1395225931
1397007931
2068448602
2069339602
2158448512
2159339512 |
2359119532
2365445632
2369009632
2456336542
2458118542
2465335642
2468008642
3067447603
3069229603
3076446703
3079119703
3157447513
3159229513
3175445713
3179009713 |
3256446523
3259119523
3265445623
3269009623
3456226543
3457117543
3465225643
3467007643
3475115743
3476006743
4067337604
4068228604
4076336704
4078118704
4086226804 |
4087117804
4158228514
4175335714
4178008714
4185225814
4187007814
4258118524
4268008624
4286006824
4365225634
4367007634
4376006734 |
3. Queen and King combinations of
palindromes vs. pandigitals
| | Palindrome | Ninedigital | | Palindrome | Pandigital | |
| | QUEEN | | KING | |
|---|
| |
630036
9530359
128909821
129808921
139707931
236909632
246808642
317909713
326909623
346707643
347606743
417808714
418707814
426808624
428606824
436707634
437606734 |
146798532
123894675
257819643
259617843
279415863
473819265
493617285
635819427
653819247
693415287
695213487
835617429
837415629
853617249
857213649
873415269
875213469 |
|
6300036
95300359
1289009821
1298008921
1397007931
2369009632
2468008642
3179009713
3269009623
3467007643
3476006743
4178008714
4187007814
4268008624
4286006824
4367007634
4376006734 |
1467908532
1238904675
2578019643
2596017843
2794015863
4738019265
4936017285
6358019427
6538019247
6934015287
6952013487
8356017429
8374015629
8536017249
8572013649
8734015269
8752013469 |
|
4. Scintillating Grid
 one pair each of digits 0, 3, 4, 6 & 7
one pair each of digits 0, 3, 4, 6 & 7
| | Palindrome | Pandigital | |
| |
0346707643
0347606743
0436707634
0437606734
3067447603
3076446703
3467007643
3476006743
4067337604
4076336704
4367007634
4376006734 |
0693415287
0695213487
0873415269
0875213469
6134895207
6152893407
6934015287
6952013487
8134675209
8152673409
8734015269
8752013469 |
|
|---|
|
For reference goals and easy searching I list here all the nine- & pandigitals implicitly displayed in these topics.
Topic 5.12 → 349512768, 365412897, 453612987, 537612984, 546913728, 652813749, 765913248, 879312546, 567914238, 897312546, 694513782, 765913428, 278415369, 825913476, 536714928, 496815237, 697514823, 435916278, 829514763, 893415267, 253817649, 294317586, 496517382, 543617289, 645917328, 874516392, 795316824, 549618237, 243618975, 537618429, 596418273, 835217469, 834917562, 236719485, 645319287, 782419356, 962718543, 469821357, 485721396, 569721384, 489621753, 597621483, 576321948, 634521987, 786321495, 879621345, 619823547, 647123589, 187524693, 745823619, 786923514, 159624837, 879623541, 916823475, 735624189, 386425179, 681324597, 419725638, 618925374, 968724513, 973524861, 897625413, 716425983, 398426715, 439527186, 974126358, 561327948, 654927831, 351628479, 391528467, 915627483, 735928146, 384629175, 163529487, 647129538, 683129745, 743129658, 851729643
1374920589, 1365920784, 1097423856, 1496723085, 1857320946, 1594823067, 1589423706, 1374925068, 1035926784, 1705823469, 1695324078, 1749623850, 1378526490, 1649725308, 1850723964, 1609825743, 1439726805, 1579826043, 1437026985, 1870524369, 1368027594, 1746925830, 1740625893
1947625380, 1938625470, 1653927408, 1467028593, 1850426379, 1986025374, 1845026793, 1590328467, 1985426073, 1458629370
576931482, 784231659, 894631527, 156932748, 519634782, 568234719, 679534812, 817534692, 925834761, 719435682
2074581639, 3986174205, 3126978405, 4973168205, 3694278105, 4698372510
3579068124, 3579068124, 2517086394, 2517086394
7512948360, 7530642918
1047629538, 1069438752, 1245703698, 1345870962, 1394870562, 1429306578, 1487960352, 1762398450, 1970538642, 2501649378, 3047618592, 3064975218, 3109765248, 3152497608, 3247051698, 3527496018, 3671045298, 3708154962, 4035972168, 4096573128, 4163098752, 4317806592, 4813570962, 5179380642, 5739061248, 5908714632, 6571394082, 7025391648, 7134629058, 7438096512, 7465931208, 7591830642, 7654803912, 7846035912, 8563740192, 9473210658, 9517032648, 9546027138, 9715064832, 9725103648, 9743521608
3921846057, 1830296457, 5032186497, 6143928570, 1486972530, 4195028637, 7162908345, 5469821370, 1972480653, 1509482673, 1357694208, 9324187605, 3061725849, 5197843620, 2537418960, 6401729853, 7914563208, 2541987360, 6528140973, 2154087693, 7256903418, 3782601954, 8104629573, 3609258714, 3268749105, 6308541972, 8417569320, 5801367492, 9421375860, 8201749365, 4692750381, 8596371240, 4317806292, 7309428165, 5372908461, 4970538261, 7863920154, 7260394581, 6879405321, 7248503961, 7853902641, 8679015234, 9027384165, 8493716052, 9862103745, 9715064832
1023849765, 1027935648, 3921846057, 7914563208, 9864025713, 9872350146, 9876135240
5678904132, 5678904132, 2690457813, 2690457813, 5490321768, 5490321768, 6029417538, 6029417538, 8576492130, 8576492130, 5047168932, 8140532769
Topic 5.9 → 132587649, 146259387, 147596823, 154768239, 168529437, 235174869, 235486197, 246875193, 248615973, 261584793, 287615493, 321845697, 384576129, 461832579, 489576213, 498162753, 815372649, 857341269, 962534781, 982461357
143857269, 147852369, 148659273, 157628493, 184967523, 247163589, 253684179, 346928751, 428571963, 456293871, 469152837, 523916487, 541786923, 546298317, 574368219, 574926183, 794823561, 798245361, 812347569, 983625147
Topic 5.7 → 124983576, 216984375
Topic 5.6 → 240545042, 2164905378, 240656042, 2165904378, 315989513, 2843905617, 360212063, 3241908567, 360989063, 3248901567, 361323163, 3251908467, 364989463, 3284905167, 420545024, 3784905216, 420656024, 3785904216, 480212084, 4321908756, 480989084, 4328901756, 485767584, 4371908256, 486989684, 4382907156, 513545315, 4621907835, 531545135, 4783906215, 531878135, 4786903215, 536989635, 4832906715, 624656426, 5621907834, 630212036, 5671908324, 630989036, 5678901324, 642656246, 5783906214, 642989246, 5786903214, 713545317, 6421907853, 724656427, 6521907843, 753878357, 6784905213, 753989357, 6785904213, 840212048, 7561908432, 840989048, 7568901432, 915989519, 8243905671, 936989639, 8432906751, 951434159, 8562907431, 951989159, 8567902431, 963878369, 8674905321, 963989369, 8675904321
Topic 5.5 → 5498162037
Topic 5.3 → 173846952, 196347852
Topic 5.2 → 3094721658, 3907415628, 4093728651, 5694317082, 5817634902, 6819320457, 6918320754, 7039428156, 8169324507, 9127436508, 9168327504, 9304765128, 9403765821
Contributions
B.S. Rangaswamy (email) - go to topic 1
B.S. Rangaswamy (email) - go to topic 2
[ TOP OF PAGE]
TOP OF PAGE]