[ November 24, 2008 ]
Multiplying Palindromes to arrive at a wheel of Pandigitals
Peter Kogel (email)

As a corollary of the topic handled in the following wonplates
WONplate 97 and WONplate 115
Peter Kogel presents now some results from
" Nine- & Pandigitals expressable as the product of two Palindromes "

smallest zeroless
252 x 489984 = 123475968
Largest zeroless
393 x 2507052 = 985271436

smallest pandigital
131 x 7814187 = 1023658497
Largest pandigital
2882 x 3420243 = 9857140326

There are several equal product examples of both types
and even a few 3-way & 4-way examples too.

252 x 489984 = 2552 x 48384 = 2772 x 44544 = 123475968
999 x 234432 = 3663 x 63936 = 6336 x 36963 = 234197568
464 x 828828 = 828 x 464464 = 4554 x 84448 = 384576192

333 x 659956 = 636 x 345543 = 6996 x 31413 = 9339 x 23532 = 219765348

Looking through the results I noticed that several palindromes appear
in more than one solution and I found a way to chain them together into
a rather pleasing palindromic/pandigital wheel (the product of any two adjacent
palindromes is pandigital). It didn't take too long to find this wheel
"by hand" so I would imagine that there are many other such examples.

I'd be interested to know what is the wheel with the largest number of members !

B.S. Rangaswamy (email) was much fascinated by the presentation made
by Peter Kogel on the 25/25 Palindromic Pandigital Wheel (see above).
He got involved in this task and was equally elated to glance through
the WONplates 97 & 115. While exploring the possibilites of a bigger wheel,
he arrived at many interesting offshoots, which he wishes to share with you
and the readers [ February 4, 2009 ] & [ March 11, 2009 ].

A. Pandigital as product of twin set of palindromes :

B. 60606 and 90909 as common factors of many pandigitals.

There exist 12 pandigitals with 60606 as one of the palindromic factors.

Click the image to get a HD illustration
[ dimensions 904 x 1190 ].

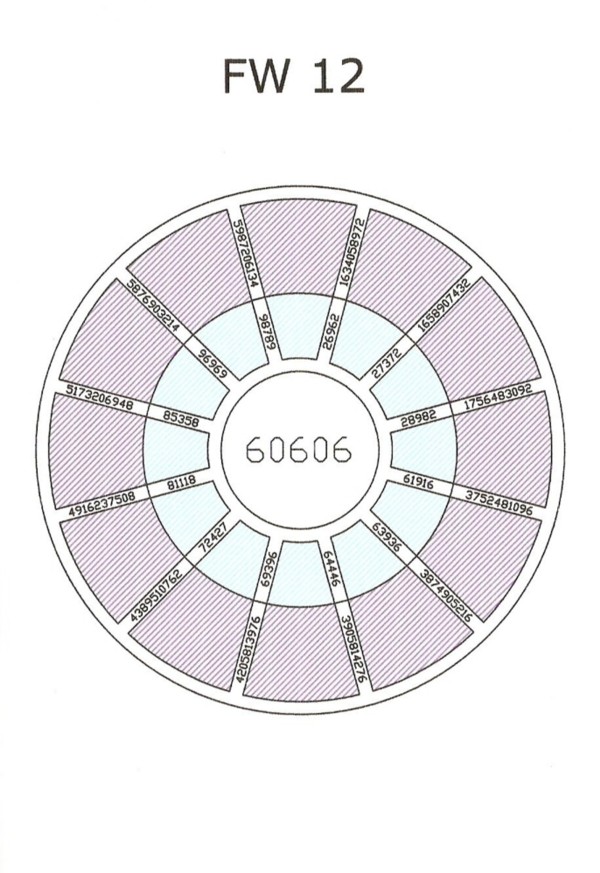
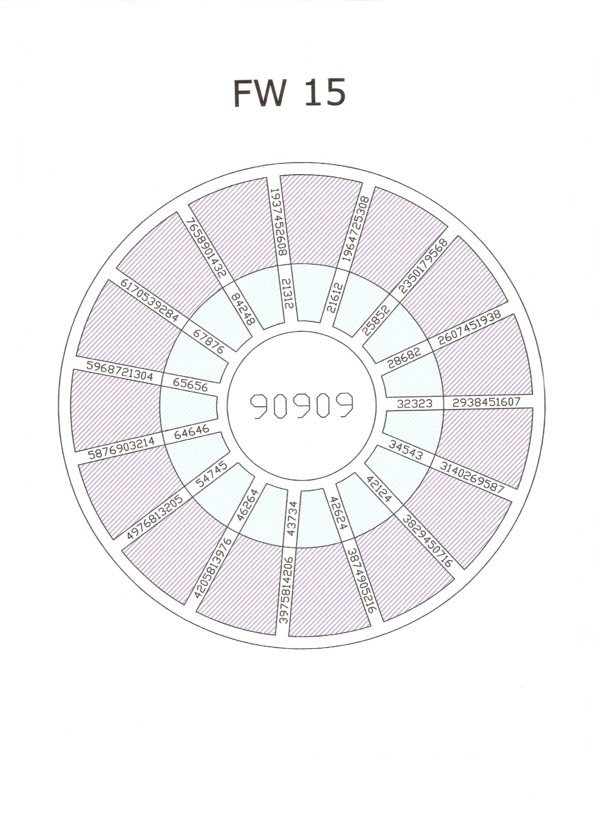
There exist 15 pandigitals with 90909 as one of the palindromic factors.

E.g. 90909 * 21312 = 1937452608

Click the image to get a HD illustration
[ dimensions 1569 x 1860 ].

C. This product of two distinct 5 digit palindromes is very enchanting,
[ 45454 * 97779 ]

as it is comprised of six fours and four sixes in a row. This has induced
me to scribe an exciting and imaginary ending of a cricket match. It may be
liked by Peter Kogel and other cricket lovers, as it is a very popular sport
in South Africa and many other parts of the World :

48 Runs for victory
Cricket may not be a familiar game in Europe, America apart from UK
and West Indies, hence some details of the game are furnished.

In the last over of the final match of a cricket tourney, the last pair
of batsmen Harrington & Warrington had to score 48 runs for a win.
This was almost an impossible task, as the present record is 36
runs in an over made by Yuvraj Singh in a T-20 match, in England.

Harrington faced the first ball of the over from bowler Solington
and scored 3 runs, but it happened to be a no ball, thus yielding
the team 4(3+1) runs. Warrington got 3 runs from the next ball,
but again it was a no ball, thus fetching his team 4(3+1) runs. Again
Harrington & Warrington got 3 runs each from 3rd and 4th balls with
consecutive no balls (one extra run per each no ball and one extra ball;
only 6 balls per over normally). Next 2 balls faced by Harrington were
dispatched to boundary fetching 4+4 runs. Each of next 4 balls were
promptly hit for sixers by Harrington, to get totally 48 runs for the
team in this most exceptional over and thus achieved a thumping victory.
Details of runs gained in this over are :

Harrington       38
Warrington       06
Extras           04
               ----
Total            48
               ----

4444446666 = 45454 * 97779

B.S.Rangaswamy, thanks for all these interesting offshoots !

Soon after a reaction came from Peter Kogel [ May 18, 2009 ]

Yes, I am indeed a great cricket fan and I am thoroughly enjoying the IPL
contest here in South Africa. We have been treated to some really amazing close
matches and some really big hitting this last week. I'm therefore not so sure your
4's & 6's cricket match commentary will remain imaginary for very much longer.
48 runs in one over might not be so far fetched afterall :o)

B.S. Rangaswamy sent me two more nice wheels [ October 5, 2012 ]

With due regards to Peter Kogel for originating the concept of PP Wheel,
herewith presenting two more wheels :

A. As an addition to my earlier list of write up on the subject -
Twin set of palindromic factors for 18 pandigitals, I have scribed a
Pandigitals/Twin palindromic factors wheel (TFW - 18) which is enclosed.
TFW-18 (PDF file)

B. A new PP-Wheel with 33333 as common Repdigital factor (FW 12A) is presented,
in addition to earlier wheels with common palindromic factors 60606 & 90909.
FW-12A (PDF file)

topic continued at wonplate 177