|
[ February 16, 2003 ]
A threefold (probable) prime search
Find the smallest prime(s) composed of the successive concatenation
of the prime factors (counting multiplicity) of the composites.
This integer sequence starts with 4 (see A002808).
| [4] | = 2 * 2 |
| [6] | = 2 * 3 |
| [8] | = 2 * 2 * 2 |
| [9] | = 3 * 3 |
| [10] | = 2 * 5 |
| [12] | = 2 * 2 * 3 |
Thus the (probable) prime(s) we are looking for begins like this
(2 * 2)(2 * 3)(2 * 2 * 2)(3 * 3)(2 * 5)(2 * 2 * 3)...
or in its pure format
22232223325223...
Note that when a next composite is added one has
to append ALL its prime factors to the string.

Secondly find similar prime(s) (>23) but this time include the
primes themselves in the composite prime factors string.
The sequence starts with 2 (see A000027 but without the unity 1).
| [2] | = prime |
| [3] | = prime |
| [4] | = 2 * 2 |
| [5] | = prime |
| [6] | = 2 * 3 |
| [7] | = prime |
| [8] | = 2 * 2 * 2 |
| [9] | = 3 * 3 |
| [10] | = 2 * 5 |
| [11] | = prime |
| [12] | = 2 * 2 * 3 |
Thus the (probable) prime(s) we are looking for begins like this
(2)(3)(2 * 2)(5)(2 * 3)(7)(2 * 2 * 2)(3 * 3)(2 * 5)(11)(2 * 2 * 3)...
or in its pure format
23225237222332511223...

Thirdly the exact exercice as above but with unity included.
| [1] | = unity |
| [2] | = prime |
| [3] | = prime |
| [4] | = 2 * 2 |
| [5] | = prime |
| [6] | = 2 * 3 |
Thus the (probable) primes we are looking for begins like this
(1)(2)(3)(2 * 2)(5)(2 * 3)...
Here are already the first three solutions
From 1 to 6
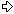 12322523 12322523
From 1 to 27
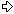 12322523... ...23222355213333 12322523... ...23222355213333
From 1 to 53
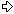 12322523... ... 472222377255317221353 12322523... ... 472222377255317221353
So what comes after 6, 27 and 53 ?

[ February 18, 2003 ]
Jeff Heleen believes to have found a prime for part 1.
Using the composite numbers from 4 to 555 (palindromic!)
gives a probable prime.
He has it running on Primo2 and should be finished
by the time he gets home (thursday nite).
" Nothing yet on parts 2 and 3 but still looking. "
[ February 25, 2003 ]
Jeff's "Primo 2.0.0 - beta 3" certificate and validation
for the number of part 1 is now available.
[PRIMO - Primality Certificate]
Version=2.0.0 - beta 3
Format=2
ID=B288601551318
Created=02/24/2003 06:12:32 AM
TestCount=291
Status=Candidate certified prime
[Candidate]
File=C:\Program Files\Primo200\Work\Arnault.in
N$=C1934B4458... ...436FD36221
HexadecimalSize=1570
DecimalSize=1891
BinarySize=6280
[Running Times]
Initialization=12.94s
1stPhase=27h 28mn 19s
2ndPhase=2h 44mn 2s
Total=30h 12mn 35s |

| ![]() TOP OF PAGE]
TOP OF PAGE]