World!Of Numbers		HOME plate WON |
The Nine Digits Page 2 with some Ten Digits (pandigital) exceptions
Page 1 Page 3 Page 4 Page 5 Page 6 Page 7

When I use the term ninedigital in these articles I always refer to a strictly zeroless pandigital (digits from 1 to 9 each appearing just once).

  Topic 2.25   [ March 1, 2000 ]
Aran Kuntze is studying the occurrences of the nine digits numbers
in the decimal expansion of  

So for instance (taken three at random from her list of 41)

Puzzle 1
Aran (from Finland) is also hoping to find a palindromic position but
had no luck so far. Can you give her a helping hand in her search ?

Puzzle 2
I propose Aran or any other puzzler to try to find a solution that occurs
at a nine digits position. Beware that it will be a hard job as one has to have
access to the first 1.000.000.000 digits of   to scan through.
The string some nine digits number was found at position some nine digits number ?

  Topic 2.24   [ February 14, 2000 ]
Once again G. L. Honaker, Jr. made an interesting discovery

This time it is about 6 primes in Arithmetic Progression
with a common difference of... our  pandigital  number !

See Sloane's A058908.

Who can construct such sequences with 7 or more primes in AP ?

  Topic 2.23  
From Felice Russo's sequence A039667

There exist only four numbers n so that
juxtaposition of  n, 2n and 3n forms a  nine digits number.

  Topic 2.22   [ September 16, 1999 ]
Two new G. L. Honaker, Jr. discoveries !

Further information
in Sloane's database : A049442, A049443 and A049446.
( see also A050278, A050288, A050289 and A050290 )
in Weisstein's Math Encyclopedia Pandigital Number.

[ November 11, 2022 ] Alexandru Petrescu explores other paths to reach more nine- and pandigital results. Here is his contribution. He discovered that the sum of the first 59295 (palindromic!) consecutive composites is a ninedigit anagram ! The sum of the first n consecutive prime numbers is a ninedigit anagram   The sum of the first n consecutive composite numbers is a ninedigit anagram   The sum of the first n consecutive prime numbers is a pandigital anagram   The sum of the first n consecutive composite numbers is a pandigital anagram n sum   n sum   n sum   n sum 8971 394521678   14829 125376498   14353 1063254978   47554 1267389504 10474 547128369   14847 125678493   18572 1829360475   49237 1358079462 10701 572469138   16895 162394758   22876 2835410967   49604 1378269450   [#3]   21146 253486197   25212 3478029561   53356 1593207684       23692 317654892   26799 3954061782   56449 1782046395       25867 378159264   27803 4271593608   56645 1794365802       28643 462983715   28752 4583260179   57328 1837624590       29389 487231695   30510 5190863247   57576 1853460927       30418 521694738   32011 5741092638   59295 1965072348       33681 638719254   32423 5897230146   62248 2164385079       34219 659143728   32515 5932401786   65250 2376809514       41292 957361482   35137 6980571324   66989 2504396871       41417 963127458   37055 7803615924   67828 2567140389       41454 964837512     [#13]   68124 2589460713         [#14]         69621 2703816459                   75626 3187265940                   79023 3478256901                   80736 3629784051                   83062 3840691257                   83875 3915807462                   87976 4305791628                   88174 4325086179                   90241 4529068317                   92224 4729156380                   92294 4736298501                   95443 5063128749                   96581 5183906247                   101059 5672914308                   104992 6120485379                   105438 6172308459                   105974 6234875019                   119684 7942058361                   122491 8316924705                   125974 8794052136                   127167 8960524713                   128445 9140586723                   130042 9368104574                   131084 9518046237                   132572 9734215086                   132614 9740351862                   132648 9745321086                     [#41]

  Topic 2.21  
An extraordinary find !

An extraordinary find by Carlos Rivera [ Visit 'PP&P' Puzzle 41 ] He succeeded in amalgamating four concepts : the Number of the Beast (666) as the quotient, the nine_digits (the numerators) the palindromes (the denominators) the primes - e.g. 1371731 versus the composites - e.g. 396693
913572846 1371731	666	264197538 396693

  Topic 2.20   [ December 12,1998 ]
Add up the values (A = 1, B = 2, C = 3, etc.) of the letters
of the written out numbers (in English)
From Carlos Rivera's Puzzle 33 of his PP&P website

A result from Carlos Rivera's work on adding the letters of written_out numbers
(in English) is that he proved that these two 9-digit numbers are equal !
The palindromic construction of the equation is a free bonus.

ONE HUNDRED TWENTY THREE MILLION FOUR HUNDRED FIFTY SIX THOUSAND SEVEN HUNDRED EIGHTY NINE
O+N+E+H+U+N+D+R+E+D+T+W+E+N+T+Y+T+H+R+E+E+M+I+L+L+I+O+N+F+O+U+R+H+U+N+D+R+E+D+F+I+F+T+Y+S+I+X+
T+H+O+U+S+A+N+D+S+E+V+E+N+H+U+N+D+R+E+D+E+I+G+H+T+Y+N+I+N+E = 964

And this value 964 is also the total of the second nine digits number !

NINE HUNDRED EIGHTY SEVEN MILLION SIX HUNDRED FIFTY FOUR THOUSAND THREE HUNDRED TWENTY ONE
N+I+N+E+H+U+N+D+R+E+D+E+I+G+H+T+Y+S+E+V+E+N+M+I+L+L+I+O+N+S+I+X+H+U+N+D+R+E+D+F+I+F+T+Y+F+O+U+R+
T+H+O+U+S+A+N+D+T+H+R+E+E+H+U+N+D+R+E+D+T+W+E+N+T+Y+O+N+E = 964
[ Quod Erat Demonstrandum  -) ]

The same method can be applied to prove that :
964 = 469 273 = 372 etc. but I leave that as an exercice for the curious puzzlers amongst you !

  Topic 2.19  
What is the 10-digits number
[from alt.math.recreational]

Source : “Mathematical Circus”, Martin Gardner, Penguin Books, 1979, p.128 & 135(solution)

In the 10 cells of the above figure inscribe a 10-digit number such that the digit in the first cell indicates the total number
of zeros in the entire number, the digit in the cell marked '1' indicates the total of 1's in the number, and so on to the last cell,
whose digit indicates the total number of 9's in the number. (zero is a digit, of course). The answer is unique.
On simple request I will mail you this unique answer (find my email address at the bottom of this page).

Number Problem #1 by QYV

Problem 4 by John Scholes

  Topic 2.18   [ November 10, 1998 ]
Puzzle : Juxtaposition of prime factors is a Nine Digits number

The puzzle questions are now :
[A] Find the largest number whereby the juxtaposition of its prime factors
is a pandigital number (the zero allowed).
[B] What are the smallest and largest juxtaposed nine digits or pandigital numbers ?
[C] What are the smallest and largest numbers for each possible 'n' prime factors whose
juxtaposition is a nine digits or pandigital numbers ?
[D] Are there nine digits or pandigital numbers whose prime factors when juxtaposed yield
another nine digits or pandigital number ?

  Topic 2.17   [ October 4, 1998 ]
Puzzle : Root Extracting Nine Digits numbers

The smallest 9-digits number so that the decimal part of its square root also starts with a 9-digits number is :

135649728^(1/2) = 11646,876319425 736908...

235916748^(1/2) =  15359,581634927 430535...
317625984^(1/3) =    682,294715863 639889...
413786925^(1/4) =    142,624518379 632388...
529638741^(1/5) =     55,564312978 124193...
613824957^(1/6) =     29,152384967 733170...
713625894^(1/7) =     18,398461752 548250...
893257614^(1/8) =     13,148375269 564618...
926374815^(1/9) =      9,915386274 757628...

[ Don't ask for solutions via e-mail as this is an open puzzle meaning I haven't a solution myself. ]
Happy hunting !

If you want to know the integers such that in the decimal representations of the square root of those integers,
the digits to the immediate right of the decimal point are 123456789 and 987654321 then visit the archives of
the Southwest Missouri State University's Problem Corner - Solution to Problem #14 !

Maybe at this point you would like to know the answer to the following
question posed by Carlos Rivera

Carlos explains his best solution for that problem (in UBASIC)

Other smaller productnumbers can easily be calculated for testing anagrams of less than 9 digits numbers. Beautiful!
Carlos, your best solution is most elegant. That way, you also found an original application for the uniqueness of primes.

  Topic 2.16  
Extracting the Nine Digits from the Number of the Beast 666

  Sum_Of_Digits{6^6} = 27      Number_Of_Digits = 5
 Sum_Of_Digits{66^66} = 531    Number_Of_Digits = 121
Sum_Of_Digits{666^666} = 8649  Number_Of_Digits = 1881 [P. De Geest]

The combination of all three numbers miraculously shows all the nine digits in a row 275318649 !
Note also that each time the numbers of digits of the next result appears to be a palindromic number.
Alas, the pattern stops with the third one because

Number_Of_Digits{6666^6666} = 25490

  Topic 2.15  
From Nine Digit Basenumbers via Nine Digit Powers arriving at Palindromes

Here is one of my recent research projects.
It makes a link between palindromes, the 'nine digits' and powers :
Task : Find a construction of the form :

whereby P is a palindromic number.
The letters A to I represent the nine digits (1 to 9) and all the nine digits must be used exactly once.
The order is unimportant.
Idem dito for the exponents a to i.

Some examples (two extremes and a random one) :

The following table shows the smallest and the largest of the 223 palindromic combinations I found.
[ In fact the search yielded exactly 211 different palindromes. ]
The third row shows a special and unique palindrome that can be written in exactly two ways
so that all the exponents differ vis-à-vis the basenumbers of the two combinations.

Smallest	12921	18 + 29 + 37 + 46 + 55 + 61 + 74 + 83 + 92
Largest	389909983	15 + 26 + 32 + 41 + 58 + 64 + 73 + 87 + 99
Special	317713	17 + 28 + 32 + 49 + 56 + 61 + 73 + 85 + 94 18 + 26 + 39 + 41 + 54 + 67 + 75 + 83 + 92

  Topic 2.14  
From Palindromes via Fibonacci arriving at Nine Digits

As palindromes are my cup of tea allow me to continue this section with them.
What I try to accomplish here is to establish a relationship between three known mathematical concepts.
Via Fibonacci iteration and starting from a palindromic number arriving at a nine digit number !
For the moment I haven't found a palindrome that transforms into 123456789 or its reversal 987654321.
In total there are 68 palindromes that yield 9-digits numbers
The smallest one is 4004 and the largest one is 437606734 ¬

1 4004 4005 8009 12014 20023 32037 52060 84097 136157 220254 356411 576665 933076 1509741 2442817 3952558 6395375 10347933 16743308 27091241 43834549 70925790 114760339 185686129 300446468 486132597 = smallest	1 630036 630037 1260073 1890110 3150183 5040293 8190476 13230769 21421245 34652014 56073259 90725273 146798532	1 1559551 1559552 3119103 4678655 7797758 12476413 20274171 32750584 53024755 85775339 138800094 224575433 363375527 587950960 951326487	1 4187814 4187815 8375629 12563444 20939073 33502517 54441590 87944107 142385697	1 4870784 4870785 9741569 14612354 24353923 38966277 63320200 102286477 165606677 267893154	1 6097906 6097907 12195813 18293720 30489533 48783253 79272786 128056039 207328825 335384864 542713689
	1 6834386 6834387 13668773 20503160 34171933 54675093 88847026 143522119 232369145 375891264	1 9530359 9530360 19060719 28591079 47651798 76242877 123894675	68 in total	1 82466428 82466429 164932857	1 437606734 437606735 875213469 = largest

[ September 11, 2005 ] Investigation and a new challenge by Carlos Rivera For your Fibonacci and Pandigital page, specially to your statement 'For the moment I haven't found a palindrome that transforms into 123456789 or its reversal 987654321.' what I can say is that NO palindrome can touch these numbers. Here are my results with some extra's as well : 15432098 15432099 30864197 46296296 77160493 123456789 61728394 61728395 123456789 493827160 493827161 987654321 110972395 110972396 221944791 332917187 554861978 887779165 1442641143 2330420308 3773061451 6103481759 9876543210 127932098 127932099 255864197 383796296 639660493 1023456789 511728394 511728395 1023456789 The only strange thing is that I was thinking that no two fibonacci series, starting with two distinct initial numbers, could hit the same number. Was I wrong ? Perhaps the statement is true for any k term of fibonacci sequence (a0, a1, a2, a3, ...) if k>2, ... Saludos. Regards.

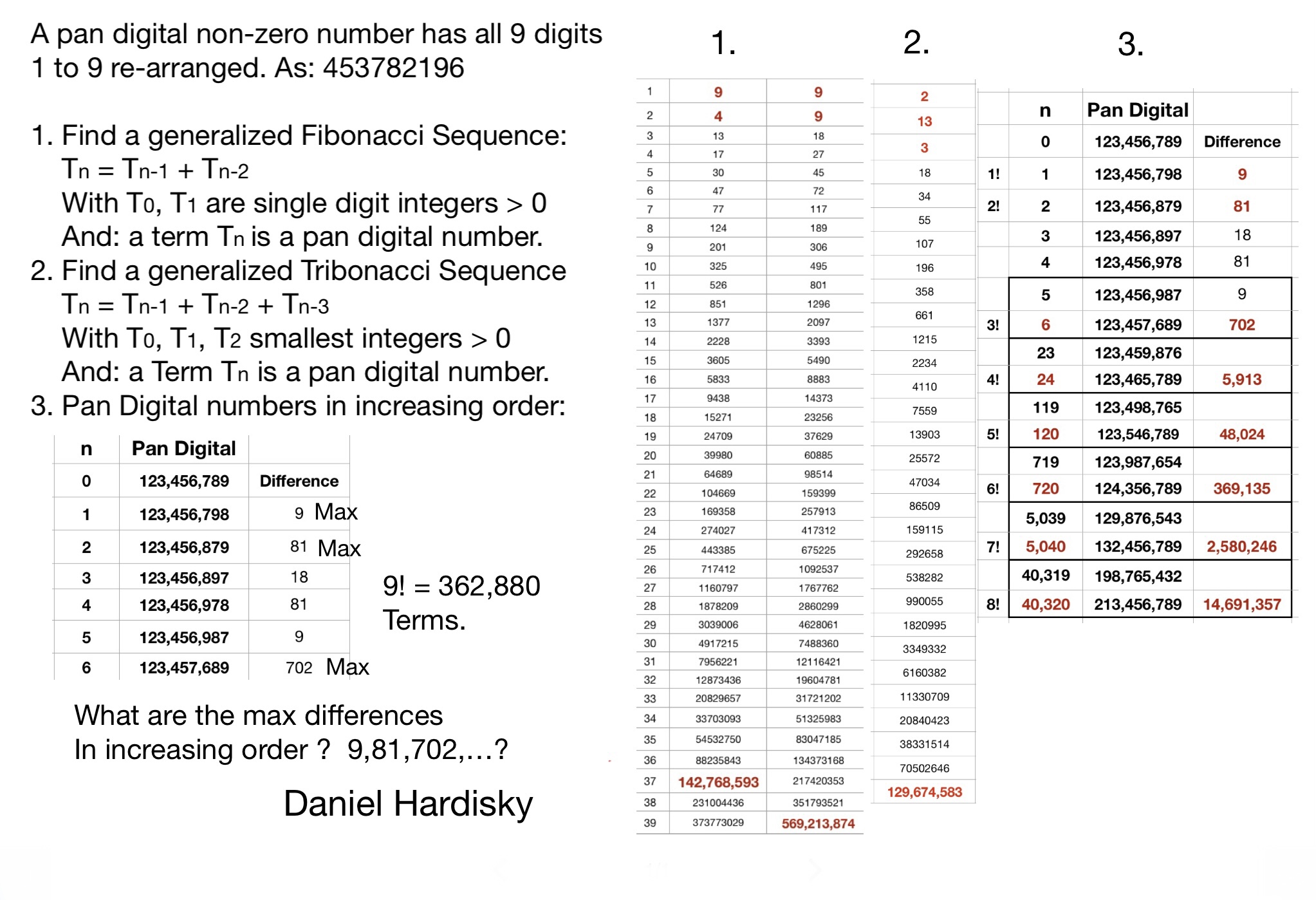
[ February 18, 2022 ] Daniel Hardisky (email) would like you to find “Generalized Fibonacci Sequences” and “Generalized Tribonacci Sequences” and find the maximum differences in increasing order. Daniel himself was surprised at the large 'gaps' between successive terms. His collage on a placard hereunder provides more information on the subject. Are you up for his challenge ?

  Topic 2.13  
Powers of ninedigitals

A small booklet called "Rekenraadsels" from Deltas vrije-tijd-reeks [1981 - ISBN 90-243-2545-5]
inspired me to start this nine digit topic.

The first two numbers multiplied together deliver a result equal to the square of another number
also containing all nine digits
246913578 x 987654312 = 493827156²
Note that 246913578 = 2 * 123456789.

Use the digits from 1 to 9 once to form two numbers, so that one number is twice the other one
6729 x 2 = 13458

There are more solutions then the one given above.
Michael Winckler published the following puzzle a while ago (Puzzle No. 121) :

  Topic 2.12  
0123456789 or pan- and ninedigital diversions

Many more digital combinations can be found in “Madachy's Mathematical Recreations” from
Joseph S. Madachy [Dover N.Y., 1979 - ISBN 0-486-23762-1, pp. 156-162]

I'll give a few excerpt to whet your appetite.
291548736 = 8 x 92 x 531 x 746
124367958 = 627 x 198354 = 9 x 26 x 531487

A square that yields all the nine digits twice !
335180136² = 112345723568978496

[ May 11, 2008 ] Investigation by Peter Kogel Hi Patrick, In Joseph Madachy's “Mathematical Recreations”  [ on page 159 ] he presents the following result and asks whether there are more results. 246913578 x 987654312 = 493827156 x 493827156 i.e. A x B = C2 where A, B and C are zero-less pandigital numbers. Not being one to allow such a challenge to pass by, I set about searching for other 9 and 10 digit pandigital examples. I was a bit disappointed to eventually discover that there are well over 12000 such solutions because this somehow seemed to dilute the aesthetic nature of the puzzle. The large number of solutions though does prove to be a veritable gold mine of supplementary results. Zero-less solutions # 620 Pandigital solutions # 6619 Mixed solutions # 5587 Total solutions # 12826 Zero-less smallest 2315976842 = 164938572 x 325196748 Zero-less largest 6594187322 = 769321854 x 897542163 Pandigital smallest 13789650422 = 1280467539 x 1485039276 Pandigital largest 83267904512 = 7450286193 x 9306412857 There are 40 examples where the sum of A and B is also zero-less and 404 examples where the sum is pandigital. E.g. the smallest for each type is : 2469135782 = 123456789 x 493827156 617283945 =  123456789 + 493827156 20539147682 = 1026957384 x 4107829536 5134786920 =  1026957384 + 4107829536 Note that the number C is actually the geometric mean of A and B ! I found that there are 36 solutions where the arithmetic mean is also pandigital. E.g.  Geometric Mean ( 1076539482, 4306157928 ) = 2153078964 Arithmetic Mean ( 1076539482, 4306157928 ) = 2691348705 There are no such solutions for zero-less numbers. There are 19 examples where both A and B are pandigital square numbers and one example where they are zero-less squares. 358532 = 1285437609   234392 = 549386721 714332 = 5102673489 x        272732 = 743816529 x 25610873492  6392518472  To the best of my knowledge these results have never been noted before. I find this surprising considering that the 30 zero-less squares and 87 pandigital squares are very well known. BTW the first square on the LHS is a palindrome ! I found two solutions where C2 is also doubly pandigital; i.e. it contains each digit twice: viz. 36729805142 = 1836490257 x 7345961028 36729805142 = 13490785856223704196 However, the second solution of this type is the 'pièce de résistance' for I was elated to note that A + B is also pandigital.               1854763209 + 7419052836 = 9273816045 37095264182 = 1854763209 x 7419052836 37095264182 = 13760586245839910724 Regards, Peter Kogel (alias Peter Pan). [ January 21, 2009 ] Reversal investigations by Peter Kogel Hi P@rick, The reversal relationship you found for the pan x pan = pal investigation (see bottom part of the webpage at twopan.htm) led me to wonder whether I couldn't use the same technique for the pan x pan = pan^2 project I ran last year (see above). I was delighted to find 6 solutions; viz: 4297315862 = 859463172 x 214865793                                         397568412 x 1590273648 = 7951368242     4935827162 = 987165432 x 246791358                                          853197642 x 3412790568 = 17063952842    13569024782 = 2713804956 x 678451239                                 932154876 x 3728619504 = 18643097522  13957026842 = 2791405368 x 697851342                                243158796 x 972635184 = 4863175922    14590273682 = 2918054736 x 729513684                                486315927 x 1945263708 = 9726318542   30975218642 = 6195043728 x 1548760932                               2390678451 x 9562713804 = 47813569022 There are also 23 solutions where the square itself can be reversed; e.g. Smallest 261845739 x 1047382956 = 5236914782                             8741963252 = 4370981625 x 174839265 Largest 175264389 x 4381609725 = 8763219452                             5491236782 = 1098247356 x 274561839 Undoubtedly best of all is the following remarkable result where each ninedigital number is reversed (unique case): Forward   Backward 159723648 846327951 x   x 489153672 276351984 =   = 2795163842 4836159722 Regards, Pete Kogel

  Topic 2.11  
I've got this from rec.puzzles

There is a 9-digit number in which the digits 1 through 9 appear exactly once.
If you only take the first N digits from the left, the number you're left with is
divisible by that same value N. What is this unique number ?

  Topic 2.10  
Ninedigital tile-layers

A tile-layer has exactly 123456789 tiles and has to make a rectangle that best approaches a neat square.
No tiles are fractured or left out. [ Dutch Source : original but dead link = http://www.win.tue.nl/math/dw/ida/h1s4.html#tegelfactor ]

He chooses this rectangle : 11409 x 10821
Can you prove that this is the best solution ?
And what if you gave our man 987654321 tiles to play with ?

  Topic 2.9  
Also from rec.puzzles

This one from a book by 'L.A. Graham'
Using all the 9 digits from 1 to 9 and only once, what two numbers multiplied
give the largest product ? Such as 12345 times 6789.

  Topic 2.8  
Source : All the Math that's Fit to Print
by Keith Devlin [ Chapter 17 p.44 ]

Arrange the digits 1 to 9 into two numbers, one of which is the square of the other.

  Topic 2.7  
A Selection of Magic Squares Websources

Magic Squares by Harvey Heinz
Magic Squares - the ultimate database by Mutsumi Suzuki
What is a Magic square ? by Allan Adler
Magic squares - Building a 9-Cell Square by Suzanne Alejandre
More than Magic squares by Ivars Peterson
Magic Square by E. Weisstein
Creating magic squares by Zimaths

Construct a Magic Square using all the digits from 1 to 9

Note that all the rows and columns and diagonals add up to 15 (fifteen).

 Visit WONplate 9 and WONplate 14 to see two beautiful Magic Squares constructed only with palindromic numbers !

  Topic 2.6  
From “All the Math that's Fit to Print”
by Keith Devlin pages 180 and 182

Find a palindrome that when multiplied with 123456789
gives a number that ends with its reversal ...987654321.

  Topic 2.5  
From “Dictionary of Curious and Interesting Numbers (revised edition 1997)”
by David Wells page 149

The minimum sum of ninedigital 3-digit primes, 149 + 263 + 587 = 999 and PALINDROMIC.
Can you find more of these fun facts beyond 149263587 ?!

  Topic 2.4  
MORELAND PI (anagram of PALINDROMES) welcomes the nine digits

Consult the 100.000.000 digits of PI and try to locate the nine digits.

This is a subtopic where I need your help. After all, of the 362.880 possible
combinations I only checked the above two...

Martin Gardner wrote a chapter about Random Numbers in his book "Mathematical Carnival".
Here's a small excerpt [ p.167 ]

... It (the brain) acquires its ability to "see" patterns only after years of experience during which
the patterned external world imposes its order on the brain's tabula rasa. It is true, of course,
that one is surprised by a sequence of 123456789 in a series of random digits because such a
sequence is defined by human mathematicians and used in counting, but there is a sense in which
such sequences correspond to the structure of the outside world...

  Topic 2.3  
Curiously this sum is palindromic and repunital

  Topic 2.2  
From the book “The Penguin Dictionary of Curious and Interesting Numbers”
Surprising facts by David Wells

  Topic 2.1  

Find a nine digit number that gives primes
whenever any one digit is dropped
This is a mathproblem once solved by Carlos Rivera

The number 123456789 is a bad example as it produces only primes when the digits 1 and 4 are dropped.
All the others are composite.

The number 987654321 is also a bad candidate as it produces only primes when the digits 2 and 5 are dropped.
All the others are composite.

Carlos Rivera came to rescue me [ July 8, 1998 ]. He wrote some code and let it ran for three hours.
As a result of this he could tell me that there are no solutions whereby 9, 8 or 7 primes shows up.
The following ninedigit number is prime '6' times when one of its digits is dropped :
126874359 ( ₁26874359, 1₂6874359, 126₈74359, 1268₇4359, 12687₄359, 1268743₅9 )
The table below displays all thirteen solutions.

[ April 17, 2022 ] Thanks, Alexandru Dan Petrescu for spotting an error in the first entry of the table
whereby the digits 2 and 6 were swapped.
When 3, 6 or 9 is dropped it produces always a multiple of 3, because every ninedigit is a multiple of 9!

David W.Wilson (email) - go to topic - [ Fri, April 10, 1998 ].

Carlos Rivera (email)   from Nuevo León, México.
- go to topic 1 - [ Wed, July 8, 1998 ].
- go to topic 2 - [ Sun, September 11, 2005 ].

Aran Kuntze (email) from Finland - go to topic - [ March 2000 ].

B.S.Rangaswamy (email) from India - go to topic - [ Januari 2007 ].

Peter Kogel (email) from South Africa - go to topic - [ May 11, 2008 ].

Peter Kogel (email) from South Africa - go to topic - [ January 21, 2009 ].

[ TOP OF PAGE]

( © All rights reserved ) - Last modified : October 3, 2023.

---

Patrick De Geest - Belgium - Short Bio - Some Pictures
E-mail address : pdg@worldofnumbers.com

---