World!Of
Numbers
HOME plate
WON |
Palindromic Merlon Primes (PMP's)
rood  1  rood  2  rood  3  rood  4  rood  5  rood  6  rood
rood Palindromic Wing Primes rood Undulating Primes rood Plateau & Depression Primes rood
rood Home Primes rood Circular Primes rood PMP-sorted

121141151171181
313323343353373
383717727747757
787919929949959
979989   


Palindromic Merlon Primes

Palindromic Merlon Primes (or PMP's for short) are numbers that
are (probable) primes, palindromic in base 10, and consisting of one central digit
(hereby named as a merlon_digit) surrounded by two symmetrical crennelations
with same digits different from the central merlon_digit and finally bordered left
and right by that same central merlon_digit. E.g.

3223223
 31111111111111111311111111111111113

From these examples you will understand the naming of these kind of palindromic primes Visualising merlons

Some links where PMP's are discussed ¬
Liczby pierwsze o szczególnym rozmieszczeniu cyfr by Andrzej Nowicki
    Translated in Dutch “Priemgetallen met een speciale rangschikking van cijfers”
    Translated in English “Prime numbers with a special arrangement of digits”
1221221 from the site 'Darkbyte'
3223223 from Prime Curios!

In case one should discover more sources I will be most happy
to add them to the list. Just let me know.

PMP's sorted by length

Some combinations can never produce primes since
these are always divisible by 3.
1(0)w1(0)w1
1(3)w1(3)w1
1(6)w1(6)w1
1(9)w1(9)w1
3(0)w3(0)w3
3(6)w3(6)w3
3(9)w3(9)w3
7(0)w7(0)w7
7(3)w7(3)w7
7(6)w7(6)w7
7(9)w7(9)w7
9(0)w9(0)w9
9(3)w9(3)w9
9(6)w9(6)w9


PMP Factorization Projects

( n = 2 * w + 3 )

PMP (Palindromic Merlon Primes) reference files.
Members can be prime.
All files maintained by Patrick De Geest.
1(2)w1(2)w1 = 2*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp121.htm  Free to factor    16 remaining  
1(4)w1(4)w1 = 4*(10n–1)/9 – 3*10n-1 – 3*10(n-1)/2 – 3 facpmp141.htm  Free to factor    12 remaining  
1(5)w1(5)w1 = 5*(10n–1)/9 – 4*10n-1 – 4*10(n-1)/2 – 4 facpmp151.htm  Free to factor    10 remaining  
1(7)w1(7)w1 = 7*(10n–1)/9 – 6*10n-1 – 6*10(n-1)/2 – 6 facpmp171.htm  Free to factor    13 remaining  
1(8)w1(8)w1 = 8*(10n–1)/9 – 7*10n-1 – 7*10(n-1)/2 – 7 facpmp181.htm  Free to factor    20 remaining  
3(1)w3(1)w3 = 3*(10n–1)/9 + 2*10n-1 + 2*10(n-1)/2 + 2 facpmp313.htm  Free to factor    14 remaining  
3(2)w3(2)w3 = 2*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp323.htm  Free to factor    12 remaining  
3(4)w3(4)w3 = 4*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp343.htm  Free to factor    13 remaining  
3(5)w3(5)w3 = 5*(10n–1)/9 – 2*10n-1 – 2*10(n-1)/2 – 2 facpmp353.htm  Free to factor    15 remaining  
3(7)w3(7)w3 = 7*(10n–1)/9 – 4*10n-1 – 4*10(n-1)/2 – 4 facpmp373.htm  Free to factor    11 remaining  
3(8)w3(8)w3 = 8*(10n–1)/9 – 5*10n-1 – 5*10(n-1)/2 – 5 facpmp383.htm  Free to factor    14 remaining  
7(1)w7(1)w7 = (10n–1)/9 + 6*10n-1 + 6*10(n-1)/2 + 6 facpmp717.htm  Free to factor    14 remaining  
7(2)w7(2)w7 = 2*(10n–1)/9 + 5*10n-1 + 5*10(n-1)/2 + 5 facpmp727.htm  Free to factor    14 remaining  
7(4)w7(4)w7 = 4*(10n–1)/9 + 3*10n-1 + 3*10(n-1)/2 + 3 facpmp747.htm  Free to factor    16 remaining  
7(5)w7(5)w7 = 5*(10n–1)/9 + 2*10n-1 + 2*10(n-1)/2 + 2 facpmp757.htm  Free to factor    18 remaining  
7(8)w7(8)w7 = 8*(10n–1)/9 – 10n-1 – 10(n-1)/2 + 2 facpmp787.htm  Free to factor    15 remaining  
9(1)w9(1)w9 = (10n–1)/9 + 8*10n-1 + 8*10(n-1)/2 + 8 facpmp919.htm  Free to factor    12 remaining  
9(2)w9(2)w9 = 2*(10n–1)/9 + 7*10n-1 + 7*10(n-1)/2 + 7 facpmp929.htm  Free to factor    13 remaining  
9(4)w9(4)w9 = 4*(10n–1)/9 + 5*10n-1 + 5*10(n-1)/2 + 5 facpmp949.htm  Free to factor    17 remaining  
9(5)w9(5)w9 = 5*(10n–1)/9 + 4*10n-1 + 4*10(n-1)/2 + 4 facpmp959.htm  Free to factor    19 remaining  
9(7)w9(7)w9 = 7*(10n–1)/9 + 2*10n-1 + 2*10(n-1)/2 + 2 facpmp979.htm  Free to factor    13 remaining  
9(8)w9(8)w9 = 8*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp989.htm  Free to factor    20 remaining  
PMP (Palindromic Merlon Primes) reference files.
Members (n>1) are always composite.
All files maintained by Patrick De Geest  [ Factorization Files Under Construction ]
1(0)w1(0)w1 = 10n + 10n/2 + 1 → (n even) facpmp101.htm  All factored (w ⩽ 100) 
1(3)w1(3)w1 = 3*(10n–1)/9 – 2.10n-1 – 2.10(n-1)/2 – 2 facpmp131.htm  Free to factor    12 remaining  
1(6)w1(6)w1 = 6*(10n–1)/9 – 5.10n-1 – 5.10(n-1)/2 – 5 facpmp161.htm  Free to factor    11 remaining  
1(9)w1(9)w1 = 9*(10n–1)/9 – 8.10n-1 – 8.10(n-1)/2 – 8 facpmp191.htm  Free to factor    5 remaining  
2(1)w2(1)w2 = (10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp212.htm  Free to factor    6 remaining  
2(3)w2(3)w2 = 3*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp232.htm  All factored (w ⩽ 100) 
2(5)w2(5)w2 = 5*(10n–1)/9 – 3*10n-1 – 3*10(n-1)/2 – 3 facpmp252.htm  Free to factor    9 remaining  
2(7)w2(7)w2 = 7*(10n–1)/9 – 5*10n-1 – 5*10(n-1)/2 – 5 facpmp272.htm  All factored (w ⩽ 100) 
2(9)w2(9)w2 = 9*(10n–1)/9 – 7*10n-1 – 7*10(n-1)/2 – 7 facpmp292.htm  Free to factor    13 remaining  
4(1)w4(1)w4 = (10n–1)/9 + 3*10n-1 + 3*10(n-1)/2 + 3 facpmp414.htm  Free to factor    12 remaining  
4(3)w4(3)w4 = 3*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp434.htm  Free to factor    11 remaining  
4(5)w4(5)w4 = 5*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp454.htm  Free to factor    12 remaining  
4(7)w4(7)w4 = 7*(10n–1)/9 – 3*10n-1 – 3*10(n-1)/2 – 3 facpmp474.htm  Free to factor    10 remaining  
4(9)w4(9)w4 = 9*(10n–1)/9 – 5*10n-1 – 5*10(n-1)/2 – 5 facpmp494.htm  Free to factor    10 remaining  
5(1)w5(1)w5 = (10n–1)/9 + 4*10n-1 + 4*10(n-1)/2 + 4 facpmp515.htm  Free to factor    13 remaining  
5(2)w5(2)w5 = 2*(10n–1)/9 + 3*10n-1 + 3*10(n-1)/2 + 3 facpmp525.htm  Free to factor    17 remaining  
5(3)w5(3)w5 = 3*(10n–1)/9 + 2*10n-1 + 2*10(n-1)/2 + 2 facpmp535.htm  Free to factor    13 remaining  
5(4)w5(4)w5 = 4*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp545.htm  Free to factor    12 remaining  
5(6)w5(6)w5 = 6*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp565.htm  Free to factor    9 remaining  
5(7)w5(7)w5 = 7*(10n–1)/9 – 2*10n-1 – 2*10(n-1)/2 – 2 facpmp575.htm  Free to factor    7 remaining  
5(8)w5(8)w5 = 8*(10n–1)/9 – 3*10n-1 – 3*10(n-1)/2 – 3 facpmp585.htm  Free to factor    10 remaining  
5(9)w5(9)w5 = 9*(10n–1)/9 – 4*10n-1 – 4*10(n-1)/2 – 4 facpmp595.htm  Free to factor    10 remaining  
6(1)w6(1)w6 = (10n–1)/9 + 5*10n-1 + 5*10(n-1)/2 + 5 facpmp616.htm  
6(5)w6(5)w6 = 5*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp656.htm  
6(7)w6(7)w6 = 7*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp676.htm  
7(3)w7(3)w7 = 3*(10n–1)/9 + 4*10n-1 + 4*10(n-1)/2 + 4 facpmp737.htm  
7(6)w7(6)w7 = 6*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp767.htm  
7(9)w7(9)w7 = 9*(10n–1)/9 – 2*10n-1 – 2*10(n-1)/2 – 2 facpmp797.htm  
8(1)w8(1)w8 = (10n–1)/9 + 7*10n-1 + 7*10(n-1)/2 + 7 facpmp818.htm  
8(3)w8(3)w8 = 3*(10n–1)/9 + 5*10n-1 + 5*10(n-1)/2 + 5 facpmp838.htm  
8(5)w8(5)w8 = 5*(10n–1)/9 + 3*10n-1 + 3*10(n-1)/2 + 3 facpmp858.htm  
8(7)w8(7)w8 = 7*(10n–1)/9 + 10n-1 + 10(n-1)/2 + 1 facpmp878.htm  
8(9)w8(9)w8 = 9*(10n–1)/9 – 10n-1 – 10(n-1)/2 – 1 facpmp898.htm  

[ February 4, 2023 ]
Chen Xinyao informs me that
https://www.alpertron.com.ar/MODFERM.HTM is the factorization of the PMPs 1(0^^w)1(0^^w)1 in base 2.

Following condition must be imposed that gcd(A,B) = 1 (in Factorization of ABB...BBABB...BBA), i.e. A and B are coprime, since if A and B have a common factor > 1, then we can divide this
factor from the number, e.g. factor 6999...9996999...9996 is equivalent to factor 2333...3332333...3332.

[ April 18, 2023 ]
Chen Xinyao informs me that
some PMPs have algebraic factors: (n=w+1)

2(3^^w)2(3^^w)2 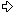3*(10^(2*n+1)-1)/9-10^(2*n)-10^n-1 = ((2^n*5^n-1)*(7*2^n*5^n+4))/3 = (1^^n) * (7(0^^(n-1)4) * 3
2(7^^w)2(7^^w)2 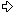7*(10^(2*n+1)-1)/9-5*10^(2*n)-5*10^n-5 = ((2^n*5^(n+1)-13)*(2^n*5^(n+1)+4))/9 = 4(9^^(n-2))87 * 5(0^^(n-1))4 / 9

I have checked all combinations of PMP, only 2333...3332333...3332 and 2777...7772777...7772 have algebraic factorization.

Thus link to Kamada's pages factorization of (1^^n), factorization of 7(0^^n)4, factorization of 2*5(0^^n)4
Unfortunately, Kamada's page has no factorization of 4(9^^n)87 or any related numbers since it only has
(x^^n), (x^^n)y, x(y^^n), (x^^n)yx, xy(x^^n), x(y^^n)x, x(y^^n)z, and (x^^n)y(x^^n).

Also 5*10^n-13 (or 4(9^^(n-2))87) is already fully factored for all n<137,
see http://factordb.com/index.php?query=5*10%5En-13&use=n&n=1&VP=on&VC=on&EV=on&OD=on&PR=on&FF=on&PRP=on&CF=on&U=on&C=on&perpage=200&format=1&sent=Show

[ February 3, 2024 ]
Patrick De Geest is always on the search for more or less beautiful patterns, curiosities and observations.

PATTERNS in the expansions of the Palindromic Merlon Numbers of type PMP545 (4*(10^(n–1))/9 + 10^(n-1) + 10^((n-1)/2) + 1) divided by a combination of its smallest factors 3, 5 & 37 with multiplicity.
Divided by 3E.g. n = 33Alternations of the digits 1, 4 and 8 except for the last digit which is a 5.181481481481481484814814814814815
Divided by 5E.g. n = 33Strings of 8's sandwiched between 10, 90 and 9. Their lengths are defined by (n-5)/2 so in this example it is 14.
Note that 10909 is a prime.		10{88888888888888}90{88888888888888}9
Divided by 3 * 3 = 9E.g. n = 33The last ten digits constitute a pandigital number 4938271605 whereby the digits from 0 to 9 are intertwined
and ascending from the right to the left →   4938271605		6049382716049382827160_4938271605
Divided by 3 * 5 = 15E.g. n = 33A string made of the digits 2, 6 and 9 squeezed between two 3's. Note it is not a palindrome.3_629629629629629696296296296296_3
Divided by 3 * 3 * 3 = 27E.g. n = 87Here also lurks a pandigital number at the end of the decimal expansion but now divided in five dispersed duo's.
…90534979423868312757201646090535		…90534979423868312757201646090535
Divided by 3 * 3 * 5 = 45E.g. n = 195All the ten digits from 0 to 9 appear at the start and the end of the decimal expansion.
Adding up 1209876543 + 0987654321 gives 2197530864 which is also a pandigital number.
And subtracting both numbers gives surprisingly 222222222 or a repdigit.		1209876543_20987654320…098765432098765432_0987654321
Divided by 3 * 37 = 111E.g. n = 27Alternations of the digits 0, 4 and 9 except for the last digit which is a 5.4904904904904994994994995
Divided by 3 * 3 * 3 * 5 = 135E.g. n = 141Nothing spectacular found except that digits 4, 5, 6, 7, 8, 9 often appear as doubles.
…0329218106 99 5 88 4 77 3 66 2 55 1 44 0329218107
Intersperced between these doubles we observe a descending sequence from digit 6 down to 0.		40329218106…0329218106995884773662551440329218107
Divided by 5 * 37 = 185E.g. n = 51Alternations of the digits 2, 4 and 9 for the left part
and 6 and 9 for the right side except for the last digit which is a 7.		2942942942942942942942942996996996996996996996997
Divided by 3 * 3 * 37 = 333E.g. n = 51Digits 2 and 7 do not appear in the decimal expansion.1634968301634968301634968331664998331664998331665
Divided by 3 * 5 * 37 = 555E.g. n = 135Alternations of only the digits 0, 8 and 9.98098098098098098098…98998998998998998999
Divided by 3 * 3 * 3 * 37 = 999E.g. n = 195Occurence of triplets like 555, 666, 777, 888, 999.
555 happens only once at the very end of the decimal expansion.		…999443888332777221666110554999443888332777221666110555
Divided by 3 * 3 * 5 * 37 = 1665E.g. n = 141Ends with a triplet of the digits 3, 6 and 9.…999666332999666332999666332_999666333
Divided by 3 * 3 * 3 * 3 * 37 = 2997E.g. n = 141I see a few triplets but nothing spectacular... Do you see more ?181663144626107589070552033514996477959440922403885366848329811292774
259073888703518333147962777592407222036851666481296110925740555370185
Divided by 3 * 3 * 3 * 5 * 37 = 4995E.g. n = 141Ends with a triplet of all the digits from 999 down to 111 separated from the rest by one zero.
…10999888777666555444333222110{999}{888}{777}{666}{555}{444}{333}{222}{111}		…10999888777666555444333222110999888777666555444333222111
Divided by 3 * 3 * 3 * 3 * 5 * 37 = 14985E.g. n = 141Again, this is a case with triplets occurring for digits 9 down to 7 and 1 to 3 upwards.
Inbetweeners 4,5,6 and 7 gather even together in quartets.
36332628925221517814110406702{999}295591{888}184480{777}073369665962258554851814{7777}
40703{6666}29592{5555}18481{4444}07370{333}296259{222}185148{111}074037		363326289252215178141104067029992955918881844807770733696659622585548
51814777740703666629592555518481444407370333296259222185148111074037

Can you reveal more intricate patterns? If so, just let me know and I'll add them also.


The “PMP” Table


The reference table for
Palindromic Merlon Primes
This collection is complete for
probable primes up to 50000
digits and for proven
primes up to  3500  digits.
PDG = Patrick De Geest
PMPFormula
blue exp = # of digits
Accolades = prime exp		WhoWhenStatusOutput
Logs
 ¬ 
   n ⩾ 50011 (PDG, September 27, 2022)
1(2)21(2)21 2*(10{7}–1)/9 – 106 – 103 – 1 PDGNov 12 2011PRIME View
1(2)41(2)41 2*(10{11}–1)/9 – 1010 – 105 – 1 PDGNov 12 2011PRIME View
1(2)111(2)111 2*(1025–1)/9 – 1024 – 1012 – 1 PDGNov 12 2011PRIME View
1(2)23921(2)23921 2*(10{4787}–1)/9 – 104786 – 102393 – 1 PDGNov 12 2011RECORD
PROVEN
PRIME		 View
1(2)188141(2)188141 2*(1037631–1)/9 – 1037630 – 1018815 – 1 PDGSep 27 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50191 (PDG, September 28, 2022)
1(4)441(4)441 4*(1091–1)/9 – 3*1090 – 3*1045 – 3 PDGNov 12 2011PRIME View
1(4)641(4)641 4*(10{131}–1)/9 – 3*10130 – 3*1065 – 3 PDGNov 12 2011PRIME View
1(4)91491(4)91491 4*(10{18301}–1)/9 – 3*1018300 – 3*109150 – 3 PDGNov 12 2011PROBABLE
PRIME		 View
1(4)228261(4)228261 4*(1045655–1)/9 – 3*1045654 – 3*1022827 – 3 PDGSep 28 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 53947 (PDG, September 28, 2022)
1(5)21(5)21 5*(10{7}–1)/9 – 4*106 – 4*103 – 4 PDGNov 12 2011PRIME View
1(5)81(5)81 5*(10{19}–1)/9 – 4*1018 – 4*109 – 4 PDGNov 12 2011PRIME View
1(5)321(5)321 5*(10{67}–1)/9 – 4*1066 – 4*1033 – 4 PDGNov 12 2011PRIME View
1(5)1281(5)1281 5*(10259–1)/9 – 4*10258 – 4*10129 – 4 PDGNov 12 2011PRIME View
1(5)4941(5)4941 5*(10{991}–1)/9 – 4*10990 – 4*10495 – 4 PDGNov 12 2011PRIME View
1(5)42611(5)42611 5*(108525–1)/9 – 4*108524 – 4*104262 – 4 PDGNov 12 2011PROBABLE
PRIME		 View
1(5)137651(5)137651 5*(1027533–1)/9 – 4*1027532 – 4*1013766 – 4 PDGSep 28 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 56095 (PDG, September 29, 2022)
1(7)41(7)41 7*(10{11}–1)/9 – 6*1010 – 6*105 – 6 PDGNov 12 2011PRIME View
1(7)221(7)221 7*(10{47}–1)/9 – 6*1046 – 6*1023 – 6 PDGNov 12 2011PRIME View
1(7)3161(7)3161 7*(10635–1)/9 – 6*10634 – 6*10317 – 6 PDGNov 12 2011PRIME View
1(7)4421(7)4421 7*(10{887}–1)/9 – 6*10886 – 6*10443 – 6 PDGNov 12 2011PRIME View
 ¬ 
   n ⩾ 58103 (PDG, September 29, 2022)
1(8)11(8)11 8*(10{5}–1)/9 – 7*104 – 7*102 – 7 PDGNov 12 2011PRIME View
1(8)21(8)21 8*(10{7}–1)/9 – 7*106 – 7*103 – 7 PDGNov 12 2011PRIME View
1(8)1451(8)1451 8*(10{293}–1)/9 – 7*10292 – 7*10146 – 7 PDGNov 12 2011PRIME View
1(8)2541(8)2541 8*(10511–1)/9 – 7*10510 – 7*10255 – 7 PDGNov 12 2011PRIME View
1(8)16271(8)16271 8*(10{3257}–1)/9 – 7*103256 – 7*101628 – 7 PDGNov 12 2011PRIME View
1(8)18131(8)18131 8*(103629–1)/9 – 7*103628 – 7*101814 – 7 PDGNov 12 2011PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 53315 (PDG, September 30, 2022)
3(1)163(1)163 (1035–1)/9 + 2*1034 + 2*1017 + 2 PDGNov 12 2011PRIME View
3(1)433(1)433 (10{89}–1)/9 + 2*1088 + 2*1044 + 2 PDGNov 12 2011PRIME View
3(1)863(1)863 (10175–1)/9 + 2*10174 + 2*1087 + 2 PDGNov 12 2011PRIME View
3(1)11533(1)11533 (10{2309}–1)/9 + 2*102308 + 2*101154 + 2 PDGNov 12 2011PRIME View
 ¬ 
   n ⩾ 50821 (PDG, October 1, 2022)
3(2)13(2)13 2*(10{5}–1)/9 + 104 + 102 + 1 PDGNov 12 2011PRIME View
3(2)23(2)23 2*(10{7}–1)/9 + 106 + 103 + 1 PDGNov 12 2011PRIME View
3(2)53(2)53 2*(10{13}–1)/9 + 1012 + 106 + 1 PDGNov 12 2011PRIME View
3(2)19033(2)19033 2*(10{3809}–1)/9 + 103808 + 101904 + 1 PDGNov 12 2011PROBABLE
PRIME		 View
3(2)29533(2)29533 2*(105909–1)/9 + 105908 + 102954 + 1 PDGNov 12 2011PROBABLE
PRIME		 View
3(2)34133(2)34133 2*(10{6829}–1)/9 + 106828 + 103414 + 1 PDGNov 12 2011PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50189 (PDG, October 2, 2022)
3(4)23(4)23 4*(10{7}–1)/9 – 106 – 103 – 1 PDGDec 27 2012PRIME View
3(4)43(4)43 4*(10{11}–1)/9 – 1010 – 105 – 1 PDGNov 12 2011PRIME View
3(4)73(4)73 4*(10{17}–1)/9 – 1016 – 108 – 1 PDGNov 12 2011PRIME View
3(4)223(4)223 4*(10{47}–1)/9 – 1046 – 1023 – 1 PDGNov 12 2011PRIME View
3(4)263(4)263 4*(1055–1)/9 – 1054 – 1027 – 1 PDGNov 12 2011PRIME View
3(4)1823(4)1823 4*(10{367}–1)/9 – 10366 – 10183 – 1 PDGNov 12 2011PRIME View
3(4)2053(4)2053 4*(10413–1)/9 – 10412 – 10206 – 1 PDGNov 12 2011PRIME View
3(4)4763(4)4763 4*(10955–1)/9 – 10954 – 10477 – 1 PDGNov 12 2011PRIME View
3(4)13193(4)13193 4*(102641–1)/9 – 102640 – 101320 – 1 PDGNov 12 2011PRIME View
3(4)127423(4)127423 4*(1025487–1)/9 – 1025486 – 1012743 – 1 PDGOct 1 2022PROBABLE
PRIME		 View
3(4)172433(4)172433 4*(1034489–1)/9 – 1034488 – 1017244 – 1 PDGOct 1 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50657 (PDG, October 2, 2022)
3(5)13(5)13 5*(10{5}–1)/9 – 2*104 – 2*102 – 2 PDGNov 12 2011PRIME View
3(5)23(5)23 5*(10{7}–1)/9 – 2*106 – 2*103 – 2 PDGNov 12 2011PRIME View
3(5)173(5)173 5*(10{37}–1)/9 – 2*1036 – 2*1018 – 2 PDGNov 12 2011PRIME View
3(5)203(5)203 5*(10{43}–1)/9 – 2*1042 – 2*1021 – 2 PDGNov 12 2011PRIME View
3(5)263(5)263 5*(1055–1)/9 – 2*1054 – 2*1027 – 2 PDGNov 12 2011PRIME View
3(5)1573(5)1573 5*(10{317}–1)/9 – 2*10316 – 2*10158 – 2 PDGNov 12 2011PRIME View
3(5)6143(5)6143 5*(10{1231}–1)/9 – 2*101230 – 2*10615 – 2 PDGNov 12 2011PRIME View
3(5)8333(5)8333 5*(10{1669}–1)/9 – 2*101668 – 2*10834 – 2 PDGNov 12 2011PRIME View
3(5)33613(5)33613 5*(106725–1)/9 – 2*106724 – 2*103362 – 2 PDGNov 12 2011PROBABLE
PRIME		 View
3(5)36313(5)36313 5*(107265–1)/9 – 2*107264 – 2*103632 – 2 PDGNov 12 2011PROBABLE
PRIME		 View
3(5)38443(5)38443 5*(10{7691}–1)/9 – 2*107690 – 2*103845 – 2 PDGNov 12 2011PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 55429 (PDG, October 3, 2022)
3(7)23(7)23 7*(10{7}–1)/9 – 4*106 – 4*103 – 4 PDGNov 12 2011PRIME View
3(7)43(7)43 7*(10{11}–1)/9 – 4*1010 – 4*105 – 4 PDGNov 12 2011PRIME View
3(7)473(7)473 7*(10{97}–1)/9 – 4*1096 – 4*1048 – 4 PDGNov 12 2011PRIME View
3(7)593(7)593 7*(10121–1)/9 – 4*10120 – 4*1060 – 4 PDGNov 12 2011PRIME View
3(7)703(7)703 7*(10143–1)/9 – 4*10142 – 4*1071 – 4 PDGNov 12 2011PRIME View
3(7)1223(7)1223 7*(10247–1)/9 – 4*10246 – 4*10123 – 4 PDGNov 12 2011PRIME View
3(7)1283(7)1283 7*(10259–1)/9 – 4*10258 – 4*10129 – 4 PDGNov 12 2011PRIME View
3(7)60943(7)60943 7*(1012191–1)/9 – 4*1012190 – 4*106095 – 4 PDGDec 4 2011PROBABLE
PRIME		 View
3(7)85243(7)85243 7*(1017051–1)/9 – 4*1017050 – 4*108525 – 4 PDGDec 4 2011PROBABLE
PRIME		 View
3(7)189893(7)189893 7*(1037981–1)/9 – 4*1037980 – 4*1018990 – 4 PDGOct 3 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50417 (PDG, October 4, 2022)
3(8)83(8)83 8*(10{19}–1)/9 – 5*1018 – 5*109 – 5 PDGNov 12 2011PRIME View
3(8)103(8)103 8*(10{23}–1)/9 – 5*1022 – 5*1011 – 5 PDGNov 12 2011PRIME View
3(8)143(8)143 8*(10{31}–1)/9 – 5*1030 – 5*1015 – 5 PDGNov 12 2011PRIME View
3(8)673(8)673 8*(10{137}–1)/9 – 5*10136 – 5*1068 – 5 PDGNov 12 2011PRIME View
3(8)3643(8)3643 8*(10731–1)/9 – 5*10730 – 5*10365 – 5 PDGNov 12 2011PRIME View
3(8)5783(8)5783 8*(101159–1)/9 – 5*101158 – 5*10579 – 5 PDGNov 12 2011PRIME View
3(8)8483(8)8483 8*(10{1699}–1)/9 – 5*101698 – 5*10849 – 5 PDGNov 12 2011PRIME View
3(8)30763(8)30763 8*(106155–1)/9 – 5*106154 – 5*103077 – 5 PDGNov 12 2011PROBABLE
PRIME		 View
3(8)78403(8)78403 8*(10{15683}–1)/9 – 5*1015682 – 5*107841 – 5 PDGDec 5 2011PROBABLE
PRIME		 View
3(8)142063(8)142063 8*(1028415–1)/9 – 5*1028414 – 5*1014207 – 5 PDGOct 3 2022PROBABLE
PRIME		 View
3(8)193993(8)193993 8*(1038801–1)/9 – 5*1038800 – 5*1019400 – 5 PDGOct 4 2022PROBABLE
PRIME		 View
3(8)233963(8)233963 8*(1046795–1)/9 – 5*1046794 – 5*1023397 – 5 PDGOct 4 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50681 (PDG, October 4, 2022)
7(1)557(1)557 (10{113}–1)/9 + 6*10112 + 6*1056 + 6 PDGNov 12 2011PRIME View
 ¬ 
   n ⩾ 51193 (PDG, October 5, 2022)
7(2)17(2)17 2*(10{5}–1)/9 + 5*104 + 5*102 + 5 PDGNov 12 2011PRIME View
7(2)47(2)47 2*(10{11}–1)/9 + 5*1010 + 5*105 + 5 PDGNov 12 2011PRIME View
7(2)77(2)77 2*(10{17}–1)/9 + 5*1016 + 5*108 + 5 PDGNov 12 2011PRIME View
7(2)227(2)227 2*(10{47}–1)/9 + 5*1046 + 5*1023 + 5 PDGNov 12 2011PRIME View
7(2)297(2)297 2*(10{61}–1)/9 + 5*1060 + 5*1030 + 5 PDGNov 12 2011PRIME View
7(2)497(2)497 2*(10{101}–1)/9 + 5*10100 + 5*1050 + 5 PDGNov 12 2011PRIME View
7(2)737(2)737 2*(10{149}–1)/9 + 5*10148 + 5*1074 + 5 PDGNov 12 2011PRIME View
7(2)837(2)837 2*(10169–1)/9 + 5*10168 + 5*1084 + 5 PDGNov 12 2011PRIME View
7(2)1187(2)1187 2*(10{239}–1)/9 + 5*10238 + 5*10119 + 5 PDGNov 12 2011PRIME View
7(2)2417(2)2417 2*(10485–1)/9 + 5*10484 + 5*10242 + 5 PDGNov 12 2011PRIME View
 ¬ 
   n ⩾ 51035 (PDG, October 5, 2022)
7(4)17(4)17 4*(10{5}–1)/9 + 3*104 + 3*102 + 3 PDGNov 12 2011PRIME View
7(4)1217(4)1217 4*(10245–1)/9 + 3*10244 + 3*10122 + 3 PDGNov 12 2011PRIME View
7(4)5207(4)5207 4*(101043–1)/9 + 3*101042 + 3*10521 + 3 PDGNov 12 2011PRIME View
7(4)12647(4)12647 4*(10{2531}–1)/9 + 3*102530 + 3*101265 + 3 PDGNov 12 2011PRIME View
7(4)17807(4)17807 4*(103563–1)/9 + 3*103562 + 3*101781 + 3 PDGNov 12 2011PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 56255 (PDG, October 5, 2022)
7(5)262727(5)262727 5*(1052547–1)/9 + 2*1052546 + 2*1026273 + 2 PDGNov 12 2011RECORD
PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 53665 (PDG, October 6, 2022)
7(8)17(8)17 8*(10{5}–1)/9 – 104 – 102 – 1 PDGNov 12 2011PRIME View
7(8)47(8)47 8*(10{11}–1)/9 – 1010 – 105 – 1 PDGNov 12 2011PRIME View
7(8)1277(8)1277 8*(10{257}–1)/9 – 10256 – 10128 – 1 PDGNov 12 2011PRIME View
7(8)3297(8)3297 8*(10{661}–1)/9 – 10660 – 10330 – 1 PDGNov 12 2011PRIME View
7(8)8037(8)8037 8*(10{1609}–1)/9 – 101608 – 10804 – 1 PDGNov 12 2011PRIME View
7(8)18407(8)18407 8*(103683–1)/9 – 103682 – 101841 – 1 PDGNov 12 2011PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50395 (PDG, October 7, 2022)
9(1)49(1)49 (10{11}–1)/9 + 8*1010 + 8*105 + 8 PDGNov 12 2011PRIME View
9(1)79(1)79 (10{17}–1)/9 + 8*1016 + 8*108 + 8 PDGNov 12 2011PRIME View
9(1)299(1)299 (10{61}–1)/9 + 8*1060 + 8*1030 + 8 PDGNov 12 2011PRIME View
9(1)469(1)469 (1095–1)/9 + 8*1094 + 8*1047 + 8 PDGNov 12 2011PRIME View
9(1)589(1)589 (10119–1)/9 + 8*10118 + 8*1059 + 8 PDGNov 12 2011PRIME View
9(1)689(1)689 (10{139}–1)/9 + 8*10138 + 8*1069 + 8 PDGNov 12 2011PRIME View
9(1)839(1)839 (10169–1)/9 + 8*10168 + 8*1084 + 8 PDGNov 12 2011PRIME View
9(1)9559(1)9559 (10{1913}–1)/9 + 8*101912 + 8*10956 + 8 PDGNov 12 2011PRIME View
9(1)11609(1)11609 (102323–1)/9 + 8*102322 + 8*101161 + 8 PDGNov 12 2011PRIME View
9(1)55049(1)55049 (10{11011}–1)/9 + 8*1011010 + 8*105505 + 8 PDGNov 12 2011PROBABLE
PRIME		 View
9(1)62689(1)62689 (10{12539}–1)/9 + 8*1012538 + 8*106269 + 8 PDGNov 12 2011PROBABLE
PRIME		 View
9(1)92909(1)92909 (10{18583}–1)/9 + 8*1018582 + 8*109291 + 8 PDGNov 12 2011PROBABLE
PRIME		 View
9(1)217669(1)217669 (1043535–1)/9 + 8*1043534 + 8*1021767 + 8 PDGOct 6 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 52841 (PDG, October 7, 2022)
9(2)49(2)49 2*(10{11}–1)/9 + 7*1010 + 7*105 + 7 PDGNov 12 2011PRIME View
9(2)89(2)89 2*(10{19}–1)/9 + 7*1018 + 7*109 + 7 PDGNov 12 2011PRIME View
9(2)269(2)269 2*(1055–1)/9 + 7*1054 + 7*1027 + 7 PDGNov 12 2011PRIME View
9(2)2029(2)2029 2*(10407–1)/9 + 7*10406 + 7*10203 + 7 PDGNov 12 2011PRIME View
9(2)20689(2)20689 2*(10{4139}–1)/9 + 7*104138 + 7*102069 + 7 PDGNov 12 2011PROBABLE
PRIME		 View
9(2)63749(2)63749 2*(1012751–1)/9 + 7*1012750 + 7*106375 + 7 PDGNov 12 2011PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 50963 (PDG, October 8, 2022)
9(4)19(4)19 4*(10{5}–1)/9 + 5*104 + 5*102 + 5 PDGNov 12 2011PRIME View
9(4)49(4)49 4*(10{11}–1)/9 + 5*1010 + 5*105 + 5 PDGNov 12 2011PRIME View
9(4)79(4)79 4*(10{17}–1)/9 + 5*1016 + 5*108 + 5 PDGNov 12 2011PRIME View
9(4)209(4)209 4*(10{43}–1)/9 + 5*1042 + 5*1021 + 5 PDGNov 12 2011PRIME View
9(4)5099(4)5099 4*(10{1021}–1)/9 + 5*101020 + 5*10510 + 5 PDGNov 12 2011PRIME View
 ¬ 
   n ⩾ 50461 (PDG, October 8, 2022)
9(5)19(5)19 5*(10{5}–1)/9 + 4*104 + 4*102 + 4 PDGNov 12 2011PRIME View
9(5)389(5)389 5*(10{79}–1)/9 + 4*1078 + 4*1039 + 4 PDGNov 12 2011PRIME View
9(5)1739(5)1739 5*(10{349}–1)/9 + 4*10348 + 4*10174 + 4 PDGNov 12 2011PRIME View
9(5)14939(5)14939 5*(102989–1)/9 + 4*102988 + 4*101494 + 4 PDGNov 12 2011PRIME View
9(5)229909(5)229919 5*(1045983–1)/9 + 4*1045982 + 4*1022991 + 4 PDGOct 8 2022PROBABLE
PRIME		 View
 ¬ 
   n ⩾ 56783 (PDG, October 8, 2022)
9(7)29(7)29 7*(10{7}–1)/9 + 2*106 + 2*103 + 2 PDGNov 12 2011PRIME View
9(7)409(7)409 7*(10{83}–1)/9 + 2*1082 + 2*1041 + 2 PDGNov 12 2011PRIME View
9(7)2989(7)2989 7*(10{599}–1)/9 + 2*10598 + 2*10299 + 2 PDGNov 12 2011PRIME View
 ¬ 
   n ⩾ 52507 (PDG, October 9, 2022)
9(8)29(8)29 8*(10{7}–1)/9 + 106 + 103 + 1 PDGNov 12 2011PRIME View
9(8)49(8)49 8*(10{11}–1)/9 + 1010 + 105 + 1 PDGNov 12 2011PRIME View
9(8)89(8)89 8*(10{19}–1)/9 + 1018 + 109 + 1 PDGNov 12 2011PRIME View
9(8)149(8)149 8*(10{31}–1)/9 + 1030 + 1015 + 1 PDGNov 12 2011PRIME View
9(8)329(8)329 8*(10{67}–1)/9 + 1066 + 1033 + 1 PDGNov 12 2011PRIME View
9(8)569(8)569 8*(10115–1)/9 + 10114 + 1057 + 1 PDGNov 12 2011PRIME View
9(8)3829(8)3829 8*(10767–1)/9 + 10766 + 10383 + 1 PDGNov 12 2011PRIME View


Sources Revealed


Neil Sloane's “Integer Sequences” Encyclopedia can be consulted online :
Neil Sloane's Integer Sequences
Various numbers, primes and palindromic primes are categorised as follows :
%N Merlon numbers. Start is identical to sequence A??????
%N Palindromic merlon primes. under A??????
%N Palindromic merlon primes exist for digitlengths a(n). under A??????
Click here to view some of the author's [P. De Geest] entries to the table.
Click here to view some entries to the table about palindromes.

Prime Curios! - site maintained by G. L. Honaker Jr. and Chris Caldwell
3223223

All probable primes above 10000 digits are also
submitted to the PRP TOP records table maintained by Henri & Renaud Lifchitz.
See : http://www.primenumbers.net/prptop/prptop.php

[up TOP OF PAGE]

( © All rights reserved ) - Last modified : November 15, 2024.
Patrick De Geest - Belgium flag - Short Bio - Some Pictures
E-mail address : pdg@worldofnumbers.com