World!Of Numbers		HOME plate WON |
Palindromic Wing Primes (PWP's) (near-repdigit palindromes)
1   2   3   4   5   6  Undulating Primes Plateau & Depression Primes Palindromic Merlon Primes Home Primes Circular Primes PWP-sorted

131	141	151	161	171
181	191	313	353	373
383	717	727	737	747
757	767	787	797	919
929	949	959	979	989

Palindromic Wing Primes (or PWP's for short) are numbers that
are primes, palindromic in base 10, and consisting of one central digit
surrounded by two wings having an equal amount of identical digits and
different from the central one. E.g.

101 99999199999 333333313333333 7777777777772777777777777 11111111111111111111111111111111411111111111111111111111111111111

While setting up this collection of palprimes I realised that perhaps
this kind of integers was already considered under another description.
And so it turned out!
Near-repunit palindromes
Near-repdigit palindromes
are the names used in the sources where I found more PWP's ¬

The Complete List of the Largest Known Primes by Chris Caldwell

The Top Ten Prime Numbers by Rudolf Ondrejka

Palindrome prime number patterns by Harvey Heinz

Liczby pierwsze o szczególnym rozmieszczeniu cyfr by Andrzej Nowicki

    Translated in Dutch “Priemgetallen met een speciale rangschikking van cijfers”

    Translated in English “Prime numbers with a special arrangement of digits”

In case one should discover more sources I will be most happy
to add them to the list. Just let me know.

---

PWP's sorted by length

---

[ October 3, 2002 ]
Harvey Dubner (email) informed me that he co-authored an article :

" I think your idea to collect PWP's is a great and worthwhile project.
Most of the work I did on this subject was included in a paper that Chris Caldwell
and I wrote that was published in the
“Journal of Recreational Mathematics”, Volume 28, No. 1, 1996-97, pp. 1-9.
With the new hardware and software that is now available it would be easy to extend
these results. You really do good work. Please keep it up."

---

[ October 4, 2002 ]
Daniel Heuer (email) started to search at the beginning of 2001 :

" You have a very good initiative. I have studied numbers of the form
p(k,n) = 10^(2n+1)–k*10^n–1 from n = 1 to 38500 and 0 < k < 10.
if k = 3, 6 or 9 p(k,n)%3 = = 0
result for other value of k is:
k = 1, n = 26, 378, 1246, 1798, 2917, 23034
k = 2, n = 118
k = 4, n = 88, 112, 198, 622, 4228, 10052
k = 5, n = 14, 22, 36, 104, 1136, 17864, 25448
k = 7, n = 1, 8, 9, 352, 530, 697, 1315, 1918, 2874, 5876, 6768
k = 8, n = 1, 5, 13, 43, 169, 181, 1579, 18077, 22652
and I am still continuing..."

---

[ December 28, 2002 ]
Jeff Heleen prime proved a record PWP with Primo.
His prime (10⁴⁷⁶⁹–1)/3 – 2*10²³⁸⁴ consists of 4769 digits.

" Here is the prime cert for (3)2384_1_(3)2384.
It finished on Christmas day.
I send in 3 parts: Primo116A, Primo116B and Primo116C.
Happy Holidays.
jeff "

Jeff positioned himself at Rank 4 in Marcel Martin's
'primo top-20' with this feat !

---

[ January 2, 2003 ]
Daniel Heuer made a new PWP world record for the new year...

"10⁹⁵⁰¹⁹–10⁴⁷⁵⁰⁹–1 is prime.
Have a good year.
Daniel "

---

[ January 14, 2003 ]
Daniel Heuer just finished scanning the provable PWP's
of the form 10²ⁿ⁺¹–k*10ⁿ–1 up to n = 50,000 (100,001 digits).
And he is continuing...
Ranges of this form are

(9)_w1(9)_w

(9)_w2(9)_w

(9)_w4(9)_w

(9)_w5(9)_w

(9)_w7(9)_w

(9)_w8(9)_w

---

[ January 27, 2003 ]
Daniel Heuer found a new PWP.

(9)₅₂₁₄₀8(9)₅₂₁₄₀    or    (10¹⁰⁴²⁸¹-1) - 10⁵²¹⁴⁰

" 10¹⁰⁴²⁸¹ – 10⁵²¹⁴⁰ –1
is the first PWP with over 100,000 digits."

---

Some nontrivial combinations can never produce primes since
these generate infinite patterns of products of two factors.

(1)_w0(1)_w = (10^w+1 + 1)(10^w - 1)/9

101 x 1 = 101 ( 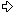is the only possible prime case when w = 1 )

1001 x 11 = 11011

10001 x 111 = 1110111

...

general formula 1(0)_k1 x 1(1)_k-21 ; ( k ⩾ 2 )

(1)_w2(1)_w = (10^w+1 - 1)(10^w + 1)/9

11 x 11 = 121

101 x 111 = 11211

1001 x 1111 = 1112111

...

general formula 1(0)_k1 x 1(1)_k1

(3)_w2(3)_w = (5.10^w + 1)(2.10^w - 1)/3

17 x 19 = 323

167 x 199 = 33233

1667 x 1999 = 3332333

...

general formula 1(6)_k7 x 1(9)_k+1

(3)_w4(3)_w = (5.10^w - 1)(2.10^w + 1)/3

7 x 49 = 343

67 x 499 = 33433

667 x 4999 = 3334333

...

general formula (6)_k7 x 4(9)_k+1

---

[ January 16, 2023 ]
Chen Xinyao draws our attention to the primes AA...AABAA...AA with A=9
The primes AA...AABAA...AA with A=9 are all proven primes (i.e. not merely probable primes),
since N+1 can be trivially near-50% factored, thus they can be proven prime using N+1 primality test
or Brillhart-Lehmer-Selfridge primality test, thus they don't need primality certificates.

---

( n = 2.w + 1 )

---

Members can be prime. (1)w3(1)w = (10n–1)/9 + 2.10(n–1)/2 Factorization of 11...11311...11 (M. Kamada) (1)w4(1)w = (10n–1)/9 + 3.10(n–1)/2 Factorization of 11...11411...11 (M. Kamada) (1)w5(1)w = (10n–1)/9 + 4.10(n–1)/2 Factorization of 11...11511...11 (M. Kamada) (1)w6(1)w = (10n–1)/9 + 5.10(n–1)/2 Factorization of 11...11611...11 (M. Kamada) (1)w7(1)w = (10n–1)/9 + 6.10(n–1)/2 Factorization of 11...11711...11 (M. Kamada) (1)w8(1)w = (10n–1)/9 + 7.10(n–1)/2 Factorization of 11...11811...11 (M. Kamada) (1)w9(1)w = (10n–1)/9 + 8.10(n–1)/2 Factorization of 11...11911...11 (M. Kamada) (3)w1(3)w = (10n–1)/3 – 2.10(n–1)/2 Factorization of 33...33133...33 (M. Kamada) (3)w5(3)w = (10n–1)/3 + 2.10(n–1)/2 Factorization of 33...33533...33 (M. Kamada) (3)w7(3)w = (10n–1)/3 + 4.10(n–1)/2 Factorization of 33...33733...33 (M. Kamada) (3)w8(3)w = (10n–1)/3 + 5.10(n–1)/2 Factorization of 33...33833...33 (M. Kamada) (7)w1(7)w = 7.(10n–1)/9 – 6.10(n–1)/2 Factorization of 77...77177...77 (M. Kamada) (7)w2(7)w = 7.(10n–1)/9 – 5.10(n–1)/2 Factorization of 77...77277...77 (M. Kamada) (7)w3(7)w = 7.(10n–1)/9 – 4.10(n–1)/2 Factorization of 77...77377...77 (M. Kamada) (7)w4(7)w = 7.(10n–1)/9 – 3.10(n–1)/2 Factorization of 77...77477...77 (M. Kamada) (7)w5(7)w = 7.(10n–1)/9 – 2.10(n–1)/2 Factorization of 77...77577...77 (M. Kamada) (7)w6(7)w = 7.(10n–1)/9 – 10(n–1)/2 Factorization of 77...77677...77 (M. Kamada) (7)w8(7)w = 7.(10n–1)/9 + 10(n–1)/2 Factorization of 77...77877...77 (M. Kamada) (7)w9(7)w = 7.(10n–1)/9 + 2.10(n–1)/2 Factorization of 77...77977...77 (M. Kamada) (9)w1(9)w = (10n–1) – 8.10(n–1)/2 Factorization of 99...99199...99 (M. Kamada) (9)w2(9)w = (10n–1) – 7.10(n–1)/2 Factorization of 99...99299...99 (M. Kamada) (9)w4(9)w = (10n–1) – 5.10(n–1)/2 Factorization of 99...99499...99 (M. Kamada) (9)w5(9)w = (10n–1) – 4.10(n–1)/2 Factorization of 99...99599...99 (M. Kamada) (9)w7(9)w = (10n–1) – 2.10(n–1)/2 Factorization of 99...99799...99 (M. Kamada) (9)w8(9)w = (10n–1) – 10(n–1)/2 Factorization of 99...99899...99 (M. Kamada)

Members (n > 1) are always composite. (1)w0(1)w = Rn * 1(0)n1 Factorization of 11...11 (Repunit) The Cunningham Project (search for 10^n-1 or 10^n+1) Factorization of 100...001 (M. Kamada) (1)w2(1)w = Rn * 1(0)n-21 Factorization of 11...11 (Repunit) The Cunningham Project (search for 10^n-1 or 10^n+1) Factorization of 100...001 (M. Kamada) (2)w1(2)w = 2.(10n–1)/9 – 10(n–1)/2 Factorization of 22...22122...22 (M. Kamada) (2)w3(2)w = 2.(10n–1)/9 + 10(n–1)/2 Factorization of 22...22322...22 (M. Kamada) (2)w5(2)w = 2.(10n–1)/9 + 3.10(n–1)/2 Factorization of 22...22522...22 (M. Kamada) (2)w7(2)w = 2.(10n–1)/9 + 5.10(n–1)/2 Factorization of 22...22722...22 (M. Kamada) (2)w9(2)w = 2.(10n–1)/9 + 7.10(n–1)/2 Factorization of 22...22922...22 (M. Kamada) (3)w2(3)w = 1(6)n7 * 1(9)n+1 Factorization of 166...667 (M. Kamada) Factorization of 199...99 (M. Kamada) (3)w4(3)w = (6)n7 * 4(9)n+1 Factorization of 66...667 (M. Kamada) Factorization of 499...99 (M. Kamada) (4)w1(4)w = [(9)n+12]/2 * (8)n9 Factorization of 99...992 (M. Kamada) Factorization of 88...889 (M. Kamada) (4)w3(4)w = 4.(10n–1)/9 – 10(n–1)/2 Factorization of 44...44344...44 (M. Kamada) (4)w5(4)w = 4.(10n–1)/9 + 10(n–1)/2 Factorization of 44...44544...44 (M. Kamada) (4)w7(4)w = [1(0)n+18]/18 * 7(9)n+1 Factorization of 100...008 (M. Kamada) Factorization of 799...99 (M. Kamada) (4)w9(4)w = 4.(10n–1)/9 + 5.10(n–1)/2 Factorization of 44...44944...44 (M. Kamada) (5)w1(5)w = 5.(10n–1)/9 – 4.10(n–1)/2 Factorization of 55...55155...55 (M. Kamada) (5)w2(5)w = 5.(10n–1)/9 – 3.10(n–1)/2 Factorization of 55...55255...55 (M. Kamada) (5)w3(5)w = 5.(10n–1)/9 – 2.10(n–1)/2 Factorization of 55...55355...55 (M. Kamada) (5)w4(5)w = 5.(10n–1)/9 – 10(n–1)/2 Factorization of 55...55455...55 (M. Kamada) (5)w6(5)w = 5.(10n–1)/9 + 10(n–1)/2 Factorization of 55...55655...55 (M. Kamada) (5)w7(5)w = 5.(10n–1)/9 + 2.10(n–1)/2 Factorization of 55...55755...55 (M. Kamada) (5)w8(5)w = 5.(10n–1)/9 + 3.10(n–1)/2 Factorization of 55...55855...55 (M. Kamada) (5)w9(5)w = 5.(10n–1)/9 + 4.10(n–1)/2 Factorization of 55...55955...55 (M. Kamada) (6)w1(6)w = 6.(10n–1)/9 – 5.10(n–1)/2 Factorization of 66...66166...66 (M. Kamada) (6)w5(6)w = 2.[8(3)n-1] * 4(0)n-11 Factorization of 833...33 (M. Kamada) Factorization of 400...001 (M. Kamada) (6)w7(6)w = 1(3)n * [1(0)n4]/2 Factorization of 133...33 (M. Kamada) Factorization of 100...004 (M. Kamada) (8)w1(8)w = 8.(10n–1)/9 – 7.10(n–1)/2 Factorization of 88...88188...88 (M. Kamada) (8)w3(8)w = 8.(10n–1)/9 – 5.10(n–1)/2 Factorization of 88...88388...88 (M. Kamada) (8)w5(8)w = 8.(10n–1)/9 – 3.10(n–1)/2 Factorization of 88...88588...88 (M. Kamada) (8)w7(8)w = 8.(10n–1)/9 – 10(n–1)/2 Factorization of 88...88788...88 (M. Kamada) (8)w9(8)w = 8.(10n–1)/9 + 10(n–1)/2 Factorization of 88...88988...88 (M. Kamada)

---

Complete list of the factorization of all possible “Palindromic Wing Numbers” can be found here Factorization of AA...AABAA...AA (M. Kamada)
with the exception of 11...11011...11, 11...11211...11, 33...33233...33, 33...33433...33, 44...44144...44, 44...44744...44, 66...66566...66 and 66...66766...66.

Following condition must be imposed that gcd(A,B) = 1, i.e. A and B are coprime, since if A and B have a common factor > 1, then we can divide this factor from the number,
e.g. factor 666...6669666...666 is equivalent to factor 222...2223222...222.

Furthermore these are not explicitly in this Makoto Kamada's page since

11...11011...11 = [ 111...111 ] * [ 1000...0001 ] and general formula R_n * 1(0)_n1 [1^^n] * [1][0^^n][1]

11...11211...11 = [ 111...111 ] * [ 1000...0001 ] and general formula R_n * 1(0)_n-21 [1^^n] * [1][0^^(n-2)][1]

33...33233...33 = [ 1666...6667 ] * [ 1999...999 ] and general formula 1(6)_n7 * 1(9)_n+1 [1][6^^n][7] * [1][9^^(n+1)]

33...33433...33 = [ 666...6667 ] * [ 4999...999 ] and general formula (6)_n7 * 4(9)_n+1 [6^^n][7] * [4][9^^(n+1)]

44...44144...44 = [ 4999...9996 ] * [ 888...8889 ] and general formula 4(9)_n6 * (8)_n9 [4][9^^n][6] * [8^^n][9]

44...44744...44 = [ 555...5556 ] * [ 7999...999 ] and general formula (5)_n6 * 7(9)_n+1 [5^^n][6] * [7][9^^(n+1)]

66...66566...66 = [ 1666...666 ] * [ 4000...0001 ] and general formula 1(6)_n * 4(0)_n-11 [1][6^^n] * [4][0^^(n-1)][1]

66...66766...66 = [ 1333...333 ] * [ 5000...0002 ] and general formula 1(3)_n * 5(0)_n-12 [1][3^^n] * [5][0^^(n-1)][2]

and their factorization [ 111...111 (Repunit) ], [ 1000...0001 ], [ 1666...6667 ], [ 1999...999 ], [ 666...6667 ], [ 4999...999 ], [ 888...8889 ], [ 7999...999 ], [ 4000...0001 ] and [ 1333...333 ] are already to be found in Kamada's pages.

Note (Chen Xinyao [ Dec 25, 2022 ] ) :
There is no factorization of 4999...9996 in Kamada's page, because [4][9^^n][6] = [9^^(n+1)][2] / 2 [ 999...9992 ]
There is no factorization of 555...5556 in Kamada's page, because [5^^n][6] = [1][0^^(n+1)][8] / 18 [ 1000...0008 ]
There is no factorization of 1666...666 in Kamada's page, because [1][6^^n] = [8][3^^(n-1)] * 2 [ 8333...333 ]
There is no factorization of 5000...0002 in Kamada's page, because [5][0^^(n-1)][2] = [1][0^^n][4] / 2 [ 1000...0004 ]

(Note: '^^' is symbol for concatenation )

---

The reference table for Palindromic Wing Primes
This collection is complete for probable primes up to 40001 digits (by DH) and for proven primes up to  3000  digits.		DB = Darren Bedwell DH = Daniel Heuer HD = Harvey Dubner JH = Jeff Heleen P&B = Propper & Batalov PDG = Patrick De Geest RP = Robert Price
PWP	Formula Blue exp = # of digits Accolades = prime exp	Who	When	Status	Output Logs
¬  ¬
(1)10(1)1	(10{3}–1)/9 – 101 IMPORTANT NOTE	PDG	Sep 23 2002	PRIME	View
A077779 ¬ A107123 ¬	[ n ⩾ 100001 ]
(1)13(1)1	(10{3}–1)/9 + 2*101	PDG	Sep 23 2002	PRIME	View
(1)23(1)2	(10{5}–1)/9 + 2*102	PDG	Sep 23 2002	PRIME	View
(1)193(1)19	(1039–1)/9 + 2*1019	PDG	Sep 23 2002	PRIME	View
(1)973(1)97	(10195–1)/9 + 2*1097	PDG	Sep 23 2002	PRIME	View
(1)98183(1)9818	(1019637–1)/9 + 2*109818	DH	Nov 04 2002	PROBABLE PRIME	View
A077780 ¬ A107124 ¬	[ n ⩾ 20001 ]
(1)24(1)2	(10{5}–1)/9 + 3*102	PDG	Sep 23 2002	PRIME	View
(1)34(1)3	(10{7}–1)/9 + 3*103	PDG	Sep 23 2002	PRIME	View
(1)324(1)32	(1065–1)/9 + 3*1032	PDG	Sep 23 2002	PRIME	View
(1)454(1)45	(1091–1)/9 + 3*1045	PDG	Sep 23 2002	PRIME	View
(1)15444(1)1544	(10{3089}–1)/9 + 3*101544	PDG	Sep 23 2002	PRIME	View DB
A077783 ¬ A107125 ¬	[ n ⩾ 200147 ]
(1)15(1)1	(10{3}–1)/9 + 4*101	PDG	Sep 23 2002	PRIME	View
(1)75(1)7	(1015–1)/9 + 4*107	PDG	Sep 23 2002	PRIME	View
(1)455(1)45	(1091–1)/9 + 4*1045	PDG	Sep 23 2002	PRIME	View
(1)1155(1)115	(10231–1)/9 + 4*10115	PDG	Sep 23 2002	PRIME	View
(1)6815(1)681	(101363–1)/9 + 4*10681	JH	Sep 29 2002	PRIME	View
(1)12485(1)1248	(102497–1)/9 + 4*101248	JH	Oct 09 2002	PRIME	View
(1)24815(1)2481	(104963–1)/9 + 4*102481	PDG	Sep 23 2002	PRIME	View
(1)26895(1)2689	(105379–1)/9 + 4*102689	PDG	Oct 11 2002	PRIME	View
(1)61985(1)6198	(1012397–1)/9 + 4*106198	DH	Oct 31 2002	PROBABLE PRIME	View
(1)131975(1)13197	(1026395–1)/9 + 4*1013197	DH	Nov 06 2002	PROBABLE PRIME	View
(1)601265(1)60126	(10120253–1)/9 + 4*1060126	RP	Oct 12 2015	PROBABLE PRIME	View
(1)1000725(1)100072	(10200145–1)/9 + 4*10100072	RP	Sep 05 2023	RECORD PROBABLE PRIME	View
A077787 ¬ A107126 ¬	[ n ⩾ 100001 ]
(1)106(1)10	(1021–1)/9 + 5*1010	PDG	Sep 23 2002	PRIME	View
(1)146(1)14	(10{29}–1)/9 + 5*1014	PDG	Sep 23 2002	PRIME	View
(1)406(1)40	(1081–1)/9 + 5*1040	PDG	Sep 23 2002	PRIME	View
(1)596(1)59	(10119–1)/9 + 5*1059	PDG	Sep 23 2002	PRIME	View
(1)1606(1)160	(10321–1)/9 + 5*10160	PDG	Sep 23 2002	PRIME	View
(1)4126(1)412	(10825–1)/9 + 5*10412	PDG	Sep 23 2002	PRIME	View
(1)5606(1)560	(101121–1)/9 + 5*10560	JH	Oct 02 2002	PRIME	View
(1)12896(1)1289	(10{2579}–1)/9 + 5*101289	JH	Oct 07 2002	PRIME	View
(1)18466(1)1846	(103693–1)/9 + 5*101846	PDG	Sep 23 2002	PRIME	View DB
A077789 ¬ A107127 ¬	[ n ⩾ 100001 ]
(1)37(1)3	(10{7}–1)/9 + 6*103	PDG	Sep 23 2002	PRIME	View
(1)337(1)33	(10{67}–1)/9 + 6*1033	PDG	Sep 23 2002	PRIME	View
(1)3117(1)311	(10623–1)/9 + 6*10311	PDG	Sep 23 2002	PRIME	View
(1)29337(1)2933	(10{5867}–1)/9 + 6*102933	JH	Jun 21 2003	PRIME	View
(1)222357(1)22235	(1044471–1)/9 + 6*1022235	RP	Apr 30 2017	PROBABLE PRIME	View
(1)391657(1)39165	(1078331–1)/9 + 6*1039165	RP	Apr 30 2017	PROBABLE PRIME	View
(1)415857(1)41585	(1083171–1)/9 + 6*1041585	RP	Apr 30 2017	PROBABLE PRIME	View
A077791 ¬ A107648 ¬	[ n ⩾ 262043 ]
(1)18(1)1	(10{3}–1)/9 + 7*101	PDG	Sep 23 2002	PRIME	View
(1)48(1)4	(109–1)/9 + 7*104	PDG	Sep 23 2002	PRIME	View
(1)68(1)6	(10{13}–1)/9 + 7*106	PDG	Sep 23 2002	PRIME	View
(1)78(1)7	(1015–1)/9 + 7*107	PDG	Sep 23 2002	PRIME	View
(1)3848(1)384	(10{769}–1)/9 + 7*10384	PDG	Sep 23 2002	PRIME	View
(1)6668(1)666	(101333–1)/9 + 7*10666	JH	Oct 02 2002	PRIME	View
(1)6758(1)675	(101351–1)/9 + 7*10675	JH	Oct 02 2002	PRIME	View
(1)31658(1)3165	(106331–1)/9 + 7*103165	DH	Oct 31 2002	PRIME	View
(1)1310208(1)131020	(10262041–1)/9 + 7*10131020	RP	Aug 03 2024	PROBABLE PRIME	View
A077795 ¬ A107649 ¬	[ n ⩾ 26621 ]
(1)19(1)1	(10{3}–1)/9 + 8*101	PDG	Sep 23 2002	PRIME	View
(1)49(1)4	(109–1)/9 + 8*104	PDG	Sep 23 2002	PRIME	View
(1)269(1)26	(10{53}–1)/9 + 8*1026	PDG	Sep 23 2002	PRIME	View
(1)1879(1)187	(10375–1)/9 + 8*10187	PDG	Sep 23 2002	PRIME	View
(1)2269(1)226	(10453–1)/9 + 8*10226	PDG	Sep 23 2002	PRIME	View
(1)8749(1)874	(101749–1)/9 + 8*10874	JH	Oct 03 2002	PRIME	View
(1)133099(1)13309	(1026619–1)/9 + 8*1013309	DH	Nov 13 2002	PROBABLE PRIME	View
A077775 ¬ A183174 ¬	[ n ⩾ 200001 ]
(3)11(3)1	(10{3}–1)/3 – 2*101	PDG	Sep 23 2002	PRIME	View
(3)31(3)3	(10{7}–1)/3 – 2*103	PDG	Sep 23 2002	PRIME	View
(3)71(3)7	(1015–1)/3 – 2*107	PDG	Sep 23 2002	PRIME	View
(3)611(3)61	(10123–1)/3 – 2*1061	PDG	Sep 23 2002	PRIME	View
(3)901(3)90	(10{181}–1)/3 – 2*1090	PDG	Sep 23 2002	PRIME	View
(3)921(3)92	(10185–1)/3 – 2*1092	PDG	Sep 23 2002	PRIME	View
(3)2691(3)269	(10539–1)/3 – 2*10269	PDG	Sep 23 2002	PRIME	View
(3)2981(3)298	(10597–1)/3 – 2*10298	PDG	Sep 23 2002	PRIME	View
(3)3211(3)321	(10{643}–1)/3 – 2*10321	PDG	Sep 23 2002	PRIME	View
(3)3711(3)371	(10{743}–1)/3 – 2*10371	PDG	Sep 23 2002	PRIME	View
(3)7761(3)776	(10{1553}–1)/3 – 2*10776	JH	Sep 28 2002	PRIME	View
(3)15671(3)1567	(103135–1)/3 – 2*101567	JH	Oct 25 2002	PRIME	View
(3)23841(3)2384	(104769–1)/3 – 2*102384	JH	Dec 25 2002	PRIME	View
(3)25661(3)2566	(105133–1)/3 – 2*102566	PDG	Sep 26 2002	PRIME	View
(3)30881(3)3088	(106177–1)/3 – 2*103088	PDG	Sep 26 2002	PRIME	View
(3)58661(3)5866	(1011733–1)/3 – 2*105866	DH	Oct 31 2002	PROBABLE PRIME	View
(3)80511(3)8051	(10{16103}–1)/3 – 2*108051	DH	Oct 31 2002	PROBABLE PRIME	View
(3)94981(3)9498	(1018997–1)/3 – 2*109498	DH	Nov 04 2002	PROBABLE PRIME	View
(3)126351(3)12635	(1025271–1)/3 – 2*1012635	DH	Nov 07 2002	PROBABLE PRIME	View
(3)245121(3)24512	(1049025–1)/3 – 2*1024512	PDG	Jul 05 2005	PROBABLE PRIME	View
(3)325211(3)32521	(1065043–1)/3 – 2*1032521	RP	Jan 29 2016	PROBABLE PRIME	View
(3)439821(3)43982	(1087965–1)/3 – 2*1043982	RP	Jan 29 2016	PROBABLE PRIME	View
A077784 ¬ A183175 ¬	[ n ⩾ 269625 ]
(3)15(3)1	(10{3}–1)/3 + 2*101	PDG	Sep 23 2002	PRIME	View
(3)25(3)2	(10{5}–1)/3 + 2*102	PDG	Sep 23 2002	PRIME	View
(3)175(3)17	(1035–1)/3 + 2*1017	PDG	Sep 23 2002	PRIME	View
(3)795(3)79	(10159–1)/3 + 2*1079	PDG	Sep 23 2002	PRIME	View
(3)1185(3)118	(10237–1)/3 + 2*10118	PDG	Sep 23 2002	PRIME	View
(3)1625(3)162	(10325–1)/3 + 2*10162	PDG	Sep 23 2002	PRIME	View
(3)1775(3)177	(10355–1)/3 + 2*10177	PDG	Sep 23 2002	PRIME	View
(3)1855(3)185	(10371–1)/3 + 2*10185	PDG	Sep 23 2002	PRIME	View
(3)2405(3)240	(10481–1)/3 + 2*10240	PDG	Sep 23 2002	PRIME	View
(3)8245(3)824	(101649–1)/3 + 2*10824	JH	Sep 29 2002	PRIME	View
(3)18205(3)1820	(103641–1)/3 + 2*101820	PDG	Sep 23 2002	PRIME	View DB
(3)23545(3)2354	(104709–1)/3 + 2*102354	PDG	Sep 23 2002	PRIME	View RC
(3)1348115(3)134811	(10{269623}–1)/3 + 2*10134811	RP	Aug 03 2024	PROBABLE PRIME	View
A077790 ¬ A183176 ¬	[ n ⩾ 235417 ]
(3)17(3)1	(10{3}–1)/3 + 4*101	PDG	Sep 23 2002	PRIME	View
(3)37(3)3	(10{7}–1)/3 + 4*103	PDG	Sep 23 2002	PRIME	View
(3)77(3)7	(1015–1)/3 + 4*107	PDG	Sep 23 2002	PRIME	View
(3)117(3)11	(10{23}–1)/3 + 4*1011	PDG	Sep 23 2002	PRIME	View
(3)137(3)13	(1027–1)/3 + 4*1013	PDG	Sep 23 2002	PRIME	View
(3)177(3)17	(1035–1)/3 + 4*1017	PDG	Sep 23 2002	PRIME	View
(3)297(3)29	(10{59}–1)/3 + 4*1029	PDG	Sep 23 2002	PRIME	View
(3)317(3)31	(1063–1)/3 + 4*1031	PDG	Sep 23 2002	PRIME	View
(3)337(3)33	(10{67}–1)/3 + 4*1033	PDG	Sep 23 2002	PRIME	View
(3)777(3)77	(10155–1)/3 + 4*1077	PDG	Sep 23 2002	PRIME	View
(3)9337(3)933	(10{1867}–1)/3 + 4*10933	JH	Oct 01 2002	PRIME	View
(3)15557(3)1555	(103111–1)/3 + 4*101555	PDG	Sep 23 2002	PRIME	View DB
(3)117587(3)11758	(1023517–1)/3 + 4*1011758	DH	Nov 13 2002	PROBABLE PRIME	View
(3)1177077(3)117707	(10235415–1)/3 + 4*10117707	RP	Oct 30 2023	PROBABLE PRIME	View
A077792 ¬ A183177 ¬	[ n ⩾ 100001 ]
(3)18(3)1	(10{3}–1)/3 + 5*101	PDG	Sep 23 2002	PRIME	View
(3)78(3)7	(1015–1)/3 + 5*107	PDG	Sep 23 2002	PRIME	View
(3)858(3)85	(10171–1)/3 + 5*1085	PDG	Sep 23 2002	PRIME	View
(3)948(3)94	(10189–1)/3 + 5*1094	PDG	Sep 23 2002	PRIME	View
(3)2738(3)273	(10{547}–1)/3 + 5*10273	PDG	Sep 23 2002	PRIME	View
(3)3568(3)356	(10713–1)/3 + 5*10356	PDG	Sep 23 2002	PRIME	View
(3)10778(3)1077	(102155–1)/3 + 5*101077	JH	Oct 11 2002	PRIME	View
(3)17978(3)1797	(103595–1)/3 + 5*101797	PDG	Sep 23 2002	PRIME	View DB
(3)67588(3)6758	(1013517–1)/3 + 5*106758	DH	Oct 31 2002	PROBABLE PRIME	View
(3)302328(3)30232	(1060465–1)/3 + 5*1030232	RP	Apr 21 2016	PROBABLE PRIME	View
¬  ¬	[ n ⩾ 200001 ] searched from july 2005 till january 2006 !
(7)1161(7)116	7*(10{233}–1)/9 – 6*10116	PDG	Sep 23 2002	PRIME	View
A077777 ¬ A183178 ¬	[ n ⩾ 100001 ]
(7)12(7)1	7*(10{3}–1)/9 – 5*101	PDG	Sep 23 2002	PRIME	View
(7)32(7)3	7*(10{7}–1)/9 – 5*103	PDG	Sep 23 2002	PRIME	View
(7)72(7)7	7*(1015–1)/9 – 5*107	PDG	Sep 23 2002	PRIME	View
(7)102(7)10	7*(1021–1)/9 – 5*1010	PDG	Sep 23 2002	PRIME	View
(7)122(7)12	7*(1025–1)/9 – 5*1012	PDG	Sep 23 2002	PRIME	View
(7)4802(7)480	7*(10961–1)/9 – 5*10480	PDG	Sep 23 2002	PRIME	View
(7)9492(7)949	7*(101899–1)/9 – 5*10949	JH	Sep 30 2002	PRIME	View
(7)19452(7)1945	7*(103891–1)/9 – 5*101945	PDG	Sep 23 2002	PRIME	View RC
(7)75482(7)7548	7*(1015097–1)/9 – 5*107548	DH	Oct 31 2002	PROBABLE PRIME	View
(7)89232(7)8923	7*(1017847–1)/9 – 5*108923	DH	Oct 31 2002	PROBABLE PRIME	View
¬  ¬	[ n ⩾ 20000 ]
(7)23(7)2	7*(10{5}–1)/9 – 4*102	PDG	Sep 23 2002	PRIME	View
A077781 ¬ A183179 ¬	[ n ⩾ 200001 ]
(7)24(7)2	7*(10{5}–1)/9 – 3*102	PDG	Sep 23 2002	PRIME	View
(7)34(7)3	7*(10{7}–1)/9 – 3*103	PDG	Sep 23 2002	PRIME	View
(7)64(7)6	7*(10{13}–1)/9 – 3*106	PDG	Sep 23 2002	PRIME	View
(7)234(7)23	7*(10{47}–1)/9 – 3*1023	PDG	Sep 23 2002	PRIME	View
(7)364(7)36	7*(10{73}–1)/9 – 3*1036	PDG	Sep 23 2002	PRIME	View
(7)694(7)69	7*(10{139}–1)/9 – 3*1069	PDG	Sep 23 2002	PRIME	View
(7)5614(7)561	7*(10{1123}–1)/9 – 3*10561	JH	Sep 28 2002	PRIME	View
(7)7234(7)723	7*(10{1447}–1)/9 – 3*10723	JH	Oct 01 2002	PRIME	View
(7)34384(7)3438	7*(106877–1)/9 – 3*103438	PDG	Oct 10 2002	PRIME	View
(7)41044(7)4104	7*(10{8209}–1)/9 – 3*104104	PDG	Oct 10 2002	PROBABLE PRIME	View
(7)90204(7)9020	7*(10{18041}–1)/9 – 3*109020	DH	Nov 04 2002	PROBABLE PRIME	View
(7)139774(7)13977	7*(1027955–1)/9 – 3*1013977	DH	Nov 13 2002	PROBABLE PRIME	View
(7)196554(7)19655	7*(1039311–1)/9 – 3*1019655	DH	Nov 25 2002	PROBABLE PRIME	View
(7)324004(7)32400	7*(1064801–1)/9 – 3*1032400	RP	Nov 23 2015	PROBABLE PRIME	View
A077785 ¬ A183180 ¬	[ n ⩾ 211221 ]
(7)15(7)1	7*(10{3}–1)/9 – 2*101	PDG	Sep 23 2002	PRIME	View
(7)75(7)7	7*(1015–1)/9 – 2*107	PDG	Sep 23 2002	PRIME	View
(7)135(7)13	7*(1027–1)/9 – 2*1013	PDG	Sep 23 2002	PRIME	View
(7)585(7)58	7*(10117–1)/9 – 2*1058	PDG	Sep 23 2002	PRIME	View
(7)1295(7)129	7*(10259–1)/9 – 2*10129	PDG	Sep 23 2002	PRIME	View
(7)2535(7)253	7*(10507–1)/9 – 2*10253	PDG	Sep 23 2002	PRIME	View
(7)16575(7)1657	7*(103315–1)/9 – 2*101657	PDG	Sep 23 2002	PRIME	View DB
(7)22445(7)2244	7*(104489–1)/9 – 2*102244	PDG	Sep 23 2002	PRIME	View DB
(7)24375(7)2437	7*(104875–1)/9 – 2*102437	PDG	Sep 23 2002	PRIME	View
(7)79245(7)7924	7*(1015849–1)/9 – 2*107924	DH	Oct 31 2002	PROBABLE PRIME	View
(7)99035(7)9903	7*(1019807–1)/9 – 2*109903	DH	Nov 04 2002	PROBABLE PRIME	View
(7)118995(7)11899	7*(1023799–1)/9 – 2*1011899	DH	Nov 05 2002	PROBABLE PRIME	View
(7)181575(7)18157	7*(1036315–1)/9 – 2*1018157	DH	Nov 18 2002	PROBABLE PRIME	View
(7)189575(7)18957	7*(1037915–1)/9 – 2*1018957	DH	Nov 20 2002	PROBABLE PRIME	View
(7)236655(7)23665	7*(1047331–1)/9 – 2*1023665	RP	Jun 25 2017	PROBABLE PRIME	View
(7)1056095(7)105609	7*(10{211219}–1)/9 – 2*10105609	RP	Oct 12 2023	PROBABLE PRIME	View
A077788 ¬ A183181 ¬	[ n ⩾ 150127 ]
(7)46(7)4	7*(109–1)/9 – 104	PDG	Sep 23 2002	PRIME	View
(7)56(7)5	7*(10{11}–1)/9 – 105	PDG	Sep 23 2002	PRIME	View
(7)86(7)8	7*(10{17}–1)/9 – 108	PDG	Sep 23 2002	PRIME	View
(7)116(7)11	7*(10{23}–1)/9 – 1011	PDG	Sep 23 2002	PRIME	View
(7)12446(7)1244	7*(102489–1)/9 – 101244	JH	Oct 16 2002	PRIME	View
(7)16856(7)1685	7*(10{3371}–1)/9 – 101685	PDG	Sep 23 2002	PRIME	View DB
(7)20096(7)2009	7*(10{4019}–1)/9 – 102009	PDG	Sep 23 2002	PRIME	View DB
(7)146576(7)14657	7*(1029315–1)/9 – 1014657	DH	Nov 13 2002	PROBABLE PRIME	View
(7)151186(7)15118	7*(1030237–1)/9 – 1015118	DH	Nov 13 2002	PROBABLE PRIME	View
(7)203326(7)20332	7*(1040665–1)/9 – 1020332	RP	Oct 07 2023	PROBABLE PRIME	View
(7)508306(7)50830	7*(10101661–1)/9 – 1050830	RP	Oct 17 2023	PROBABLE PRIME	View
(7)750626(7)75062	7*(10150125–1)/9 – 1075062	RP	Dec 7 2023	PROBABLE PRIME	View
A077793 ¬ A183182 ¬	[ n ⩾ 227777 ]
(7)18(7)1	7*(10{3}–1)/9 + 101	PDG	Sep 23 2002	PRIME	View
(7)38(7)3	7*(10{7}–1)/9 + 103	PDG	Sep 23 2002	PRIME	View
(7)398(7)39	7*(10{79}–1)/9 + 1039	PDG	Sep 23 2002	PRIME	View
(7)548(7)54	7*(10{109}–1)/9 + 1054	PDG	Sep 23 2002	PRIME	View
(7)1688(7)168	7*(10{337}–1)/9 + 10168	PDG	Sep 23 2002	PRIME	View
(7)2408(7)240	7*(10481–1)/9 + 10240	PDG	Sep 23 2002	PRIME	View
(7)53288(7)5328	7*(10{10657}–1)/9 + 105328	DH	Oct 31 2002	PROBABLE PRIME	View
(7)61598(7)6159	7*(1012319–1)/9 + 106159	DH	Oct 31 2002	PROBABLE PRIME	View
(7)246758(7)24675	7*(1049351–1)/9 + 1024675	RP	Oct 07 2023	PROBABLE PRIME	View
(7)522278(7)52227	7*(10104455–1)/9 + 1052227	RP	Oct 30 2023	PROBABLE PRIME	View
(7)1138878(7)113887	7*(10227775–1)/9 + 10113887	RP	Aug 03 2024	PROBABLE PRIME	View
A077796 ¬ A183183 ¬	[ n ⩾ 100001 ]
(7)19(7)1	7*(10{3}–1)/9 + 2*101	PDG	Sep 23 2002	PRIME	View
(7)29(7)2	7*(10{5}–1)/9 + 2*102	PDG	Sep 23 2002	PRIME	View
(7)89(7)8	7*(10{17}–1)/9 + 2*108	PDG	Sep 23 2002	PRIME	View
(7)199(7)19	7*(1039–1)/9 + 2*1019	PDG	Sep 23 2002	PRIME	View
(7)209(7)20	7*(10{41}–1)/9 + 2*1020	PDG	Sep 23 2002	PRIME	View
(7)2129(7)212	7*(10425–1)/9 + 2*10212	PDG	Sep 23 2002	PRIME	View
(7)2809(7)280	7*(10561–1)/9 + 2*10280	PDG	Sep 23 2002	PRIME	View
(7)8879(7)887	7*(101775–1)/9 + 2*10887	JH	Oct 03 2002	PRIME	View
(7)10219(7)1021	7*(102043–1)/9 + 2*101021	JH	Oct 04 2002	PRIME	View
(7)55159(7)5515	7*(1011031–1)/9 + 2*105515	DH	Oct 31 2002	PROBABLE PRIME	View
(7)81169(7)8116	7*(1016233–1)/9 + 2*108116	DH	Oct 31 2002	PROBABLE PRIME	View
(7)118529(7)11852	7*(1023705–1)/9 + 2*1011852	DH	Nov 05 2002	PROBABLE PRIME	View
A077776 ¬ A183184 ¬	[ n ⩾ 68001 ]
(9)11(9)1	(10{3}–1) – 8*101	PDG	Sep 23 2002	PRIME	View
(9)51(9)5	(10{11}–1) – 8*105	PDG	Sep 23 2002	PRIME	View
(9)131(9)13	(1027–1) – 8*1013	PDG	Sep 23 2002	PRIME	View
(9)431(9)43	(1087–1) – 8*1043	PDG	Sep 23 2002	PRIME	View
(9)1691(9)169	(10339–1) – 8*10169	PDG	Sep 23 2002	PRIME	View
(9)1811(9)181	(10363–1) – 8*10181	PDG	Sep 23 2002	PRIME	View
(9)15791(9)1579	(103159–1) – 8*101579	PDG	Sep 23 2002	PRIME	View
(9)180771(9)18077	(1036155–1) – 8*1018077	DH	Jul 21 2001	PRIME	View
(9)226521(9)22652	(1045305–1) – 8*1022652	DH	Sep 18 2001	PRIME	View
(9)1573631(9)157363	(10314727–1) – 8*10157363	DB	Jan 8 2013	PRIME	View
A077778 ¬ A115073 ¬	[ n ⩾ 68001 ]
(9)12(9)1	(10{3}–1) – 7*101	PDG	Sep 23 2002	PRIME	View
(9)82(9)8	(10{17}–1) – 7*108	PDG	Sep 23 2002	PRIME	View
(9)92(9)9	(10{19}–1) – 7*109	PDG	Sep 23 2002	PRIME	View
(9)3522(9)352	(10705–1) – 7*10352	PDG	Sep 23 2002	PRIME	View
(9)5302(9)530	(10{1061}–1) – 7*10530	JH	Sep 28 2002	PRIME	View
(9)6972(9)697	(101395–1) – 7*10697	JH	Sep 28 2002	PRIME	View
(9)13152(9)1315	(102631–1) – 7*101315	HD	––– –– 1989	PRIME	View
(9)19182(9)1918	(103837–1) – 7*101918	HD	––– –– 1999	PRIME	View
(9)28742(9)2874	(10{5749}–1) – 7*102874	HD	––– –– 1999	PRIME	View
(9)58762(9)5876	(1011753–1) – 7*105876	HD	––– –– 1999	PRIME	View
(9)67682(9)6768	(10{13537}–1) – 7*106768	HD	––– –– 1999	PRIME	View
(9)629382(9)62938	(10125877–1) – 7*1062938	DB	Oct 31 2010	PRIME	View
(9)1347392(9)134739	(10269479–1) – 7*10134739	DB	Feb 29 2012	PRIME	View
A077782 ¬ A183185 ¬	[ n ⩾ 68001 ]
(9)144(9)14	(10{29}–1) – 5*1014	PDG	Sep 23 2002	PRIME	View
(9)224(9)22	(1045–1) – 5*1022	PDG	Sep 23 2002	PRIME	View
(9)364(9)36	(10{73}–1) – 5*1036	PDG	Sep 23 2002	PRIME	View
(9)1044(9)104	(10209–1) – 5*10104	PDG	Sep 23 2002	PRIME	View
(9)11364(9)1136	(10{2273}–1) – 5*101136	JH	Oct 13 2002	PRIME	View
(9)178644(9)17864	(10{35729}–1) – 5*1017864	DH	Jul 02 2001	PRIME	View
(9)254484(9)25448	(1050897–1) – 5*1025448	DH	Oct 29 2001	PRIME	View
A077786 ¬ A183186 ¬	[ n ⩾ 68001 ]
(9)885(9)88	(10177–1) – 4*1088	PDG	Sep 23 2002	PRIME	View
(9)1125(9)112	(10225–1) – 4*10112	PDG	Sep 23 2002	PRIME	View
(9)1985(9)198	(10{397}–1) – 4*10198	PDG	Sep 23 2002	PRIME	View
(9)6225(9)622	(101245–1) – 4*10622	JH	Oct 02 2002	PRIME	View
(9)42285(9)4228	(108457–1) – 4*104228	PDG	Oct 04 2002	PRIME	View
(9)100525(9)10052	(1020105–1) – 4*1010052	DH	Mar 28 2001	PRIME	View
(9)558625(9)55862	(10111725–1) – 4*1055862	DB	Sep 19 2010	PRIME	View
¬  ¬	[ n ⩾ 68000 ]
(9)1187(9)118	(10237–1) – 2*10118	PDG	Sep 23 2002	PRIME	View
(9)1451267(9)145126	(10290253–1) – 2*10145126	DB	Apr 11 2012	PRIME	View
A077794 ¬ A183187 ¬	[ n ⩾ 68001 ]
(9)268(9)26	(10{53}–1) – 1026	PDG	Sep 23 2002	PRIME	View
(9)3788(9)378	(10{757}–1) – 10378	PDG	Sep 23 2002	PRIME	View
(9)12468(9)1246	(102493–1) – 101246	HD	––– –– 1989	PRIME	View
(9)17988(9)1798	(103597–1) – 101798	PDG	Sep 23 2002	PRIME	View
(9)29178(9)2917	(105835–1) – 102917	PDG	Oct 04 2002	PRIME	View
(9)230348(9)23034	(1046069–1) – 1023034	DH	Sep 22 2001	PRIME	View
(9)475098(9)47509	(1095019–1) – 1047509	DH	Jan 02 2003	PRIME	View
(9)521408(9)52140	(10{104281}–1) – 1052140	DH	Jan 27 2003	PRIME	View
(9)674048(9)67404	(10134809–1) – 1067404	DB	Nov 24 2010	PRIME	View
(9)9442648(9)944264	(101888529–1) – 10944264	P&B	Oct 18 2021	RECORD PROVEN PRIME	View

[ July 8, 2023 ]
Data table for the PWP's becoming prime when removing all the prime factors 2 and 5.
By Xinyao Chen.

Form	prime at n
(2^^k)1(2^^k)/(2^1)	3, 4, 9, 22, 25, 52, 55, 129, 193, 289, ...
(2^^k)3(2^^k)/(2^1)	2, 13, 23, 55, 484, 539, ...
(2^^k)5(2^^k)/(2^1)	2, 3, 5, 6, 8, 9, 20, 86, 89, 177, 260, ...
(2^^k)7(2^^k)/(2^1)	16, ...
(2^^k)9(2^^k)/(2^1)	4, 5, 11, 71, 91, 119, 176, 181, ...
(4^^k)1(4^^k)/(2^2)	none exists (algebraic factorization)
(4^^k)3(4^^k)/(2^2)	20, 130, 245, 251, 527, ...
(4^^k)5(4^^k)/(2^2)	3, 7, 9, ...
(4^^k)7(4^^k)/(2^2)	none exists (algebraic factorization)
(4^^k)9(4^^k)/(2^2)	14, 16, 22, 542, 731, ...
(5^^k)1(5^^k)/(5^1)	1, 3, ...
(5^^k)2(5^^k)/(5^1)	8, 9, 11, 15, 33, 462, 537, ...
(5^^k)3(5^^k)/(5^1)	1, 2, 7, 517, ...
(5^^k)4(5^^k)/(5^1)	1, 4, 10, 12, 33, 79, 387, 546, ...
(5^^k)6(5^^k)/(5^1)	1, 2, 4, 19, 40, 77, 124, 193, 197, 355, 586, 875, ...
(5^^k)7(5^^k)/(5^1)	73, 775, ...
(5^^k)8(5^^k)/(5^1)	2, 3, 8, 57, 65, 158, 300, ...
(5^^k)9(5^^k)/(5^1)	8, 10, 11, 158, ...
(6^^k)1(6^^k)/(2^1)	2, 4, 70, 88, 254, ...
(6^^k)5(6^^k)/(2^1)	none exists (algebraic factorization)
(6^^k)7(6^^k)/(2^1)	none exists (algebraic factorization)
(8^^k)1(8^^k)/(2^3)	85, 127, 220, 780, ...
(8^^k)3(8^^k)/(2^3)	13, 19, ...
(8^^k)5(8^^k)/(2^3)	6, 816, 818, ...
(8^^k)7(8^^k)/(2^3)	4, 123, 547, 676, ...
(8^^k)9(8^^k)/(2^3)	10, ...

Neil Sloane's “Integer Sequences” Encyclopedia can be consulted online : Neil Sloane's Integer Sequences Various numbers, primes and palindromic primes are categorised as follows : %N Wing numbers. Start is identical to sequence A046075 %N Palindromic wing primes. under A077798 %N Palindromic wing primes exist for digitlengths a(n). under A077797 Wing numbers otherwise ordered by its wing digit and not its central digit by Amarnath Murthy %N a(1) = 11; for n > 1, palindromic primes in which a single digit is sandwiched between strings of '1's. A088281 %N a(1) = 11; for n > 1, palindromic primes in which a single digit is sandwiched between strings of '3's. A088282 %N a(1) = 11; for n > 1, palindromic primes in which a single digit is sandwiched between strings of '7's. A088283 %N a(1) = 11; for n > 1, palindromic primes in which a single digit is sandwiched between strings of '9's. A088284 Click here to view some of the author's [P. De Geest] entries to the table. Click here to view some entries to the table about palindromes.

Prime Curios! - site maintained by G. L. Honaker Jr. and Chris Caldwell

101

131

151

181

191

313

353

373

383

727

757

787

797

919

929

11311

1114111

1115111

111181111

777767777

77777677777

99999199999

1111118111111

11111...5...11111 (91-digits)

77777...8...77777 (109-digits)

77777...2...77777 (961-digits)

99999...2...99999 (1061-digits)

99999...8...99999 (2493-digits)

99999...2...99999 (2631-digits)

99999...2...99999 (5749-digits)

All of Daniel Heuer's probable primes above 10000 digits are also
submitted to the PRP TOP records table maintained by Henri & Renaud Lifchitz.
See : http://www.primenumbers.net/prptop/prptop.php

---

[ TOP OF PAGE]

---

( © All rights reserved ) - Last modified : August 4, 2024.

---

Patrick De Geest - Belgium - Short Bio - Some Pictures
E-mail address : pdg@worldofnumbers.com

---